トップ
《 改定 第1章 ―第3ステップ― 》
第3ステップでは、〈物体を代表する点〉の位置が時間の関数として与えられているとき、その点の速度と加速度を算定する方法を述べます。速度と加速度を定義するときには、微分法と積分法の手法が用いられます。
微小変位、および、平均速度
空間の点の位置が時間の経過とともに変化することを「変位」といい、〈物体を代表する点〉が変位する有様を前ページの〔 図 1-9 〕に示しました(
の 変位、および、変位ベクトル を参照 )。微小な時間における変位を、「微小変位」と呼ぶことにします。
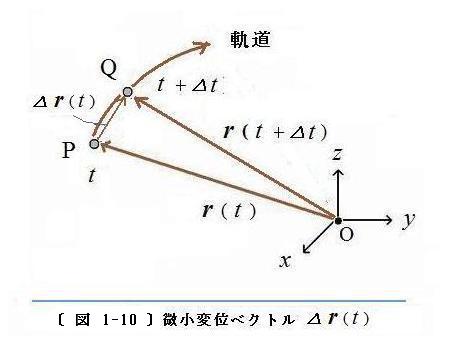 〔 図 1-10 〕
〔 図 1-10 〕 に示すように、時刻
t から微小時間
△t 経過した
t +
△t までの間に〈物体を代表する点〉が軌道に沿って空間の 点P から Q の位置に移動したとします。
軌道上の P と Q の位置を表す位置ベクトルを
r(
t) および
r(
t+
△t) としたとき、変位ベクトル
△r は代数式で
△r =
r(
t+
△t)-
r(
t)
( 変位ベクトル )
と表されます(
の ベクトルの演算 を参照 )。
上記の式(
( 変位ベクトル ))の両辺を、二つの時刻の時間間隔
△t で割ります。割り算は(1/
△t)と表されるので、この演算は〝ベクトルとスカラーの積〟になり、演算した結果はベクトルになります(
の ベクトルの演算(2) を参照 )。
左辺の
△r /
△t を『 時刻
t から時刻
t+
△t までの間の
平均速度(
mean velocity )』といい、これを
v mean と表します。ゆえに
v mean = △r/△t = { r(t+△t)- r(t) }/△t ( 平均速度 )
となります。平均速度の方向は変位ベクトルの方向と同じです。すなわち、〔 図 1-10 〕で P から Q に向かう方向になります。平均速度の大きさは、
|△r|/△t = { PQ 間の距離 }/{ 微小な時間間隔 } となります。
◇ v は 速度 velocity の頭文字をとったもので、右肩の添字 mean は〝平均の〟という意味の英語です。
平均速度の意味を明らかにするために、〔 図 1-10 〕において、時刻
t の同時刻に P を出発して次の経路を進む 点 a と b の運動を考えてみます:
〇 a は軌道に沿って進み、b は 線分PQ に沿って真直ぐに進みます。時刻 t + △t で a と b は同時に Q に到達します。
〇 a は軌道に沿って進むので、その速さや向きは時間とともに少しづつ変化します。
〇 b は同じ方向に同じ速さで進みますが、この b の進む向きと速さが「平均速度」です。
二つの点の a と b が時々刻々に進む速さと方向はわずかづつ異なりますが、時間間隔
△t が小さくなるほど、両者の違いは少なくなります。すなわち、変位が微小になるほど a の運動は b の運動でより良く近似されるようになります。
平均速度の大きさは 〝 {空間の2点間の距離}/{時間}〟の単位で表され、 国際単位系(SI)を用いると
[m/s]
( 平均速度の単位 )
となります。
速度
上記の
( 平均速度 ) の式
v mean =
△r/
△t = {
r(
t+
△t)-
r(
t)}/
△t において、
△t の大きさを小さくしてゆき、最終的に 0(
ゼロ )に移行させた極限ではどうなるでしょうか。なお、
△t を 0 に移行させる操作を
△t → 0 と表します。
平均速度はベクトルであり、大きさと方向を持つ量です。そこで
△t → 0 の極限において、平均速度が収束する 大きさと方向 を知る必要があります。〔 図 1-10 〕を見ながらこれを調べてみます。
◇ 平均速度の大きさは |△r|/△t です。△t を 0 に近づけると、PQ 間の距離|△r| も 0 に近づきます。△t → 0 の極限において、この比|△r|/△t は一定の量に収束するものと仮定し、収束した量を「速度の大きさ」と定義します。式で表せば
速度の大きさ = lim △t → 0 (|△r|/△t) ( 速度の大きさ )
となります。右辺の lim △t → 0 は、後の括弧( )の中の量を △t → 0 の極限に移行させるという記号です。
◇ 平均速度の方向は、ベクトル △r の方向と同じです。〔 図 1-10 〕で △t を小さくしてゆくと、△r の終点 Q は軌道に沿って P の位置に近づきます。△t → 0 の極限では、△r の方向は P の位置における〝軌道の 接線方向〟に収束することが分かります。平均速度の方向が △t → 0 の極限で収束する方向のことを「速度の方向」と定義します。すなわち
速度の方向 = P の位置における軌道の接線方向 ( 速度の方向 )
となります。
こうして得られる
( 速度の大きさ ) と
( 速度の方向 ) を併せたベクトルを
速度(
velocity )といい、これを記号の
v で表します。式で表せば
v = lim △t → 0 ( △r/△t) = lim △t → 0 { r(t+△t)- r(t)}/△t ( 速度 )
となります。
速度の定義から明らかなように、
△t → 0 の極限で得られる
v は、時刻
t における速度であることが分かります。時刻の
t は任意の時間に選べるので、
v は時間
t の関数と見なすことができます。これを明示すれば
v(
t)
となります。
速度の単位は平均速度と同じで、国際単位系(SI)で
[m/s]
( 速度の単位 )
となります。
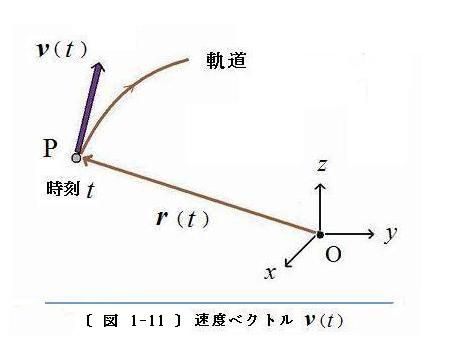
〔 図 1-11 〕 に、時刻
t における速度ベクトル
v(
t)(
紫色の矢印付きの線分 ) および 位置ベクトル
r(
t)(
茶色の矢印付きの線分 ) を示します。
v(
t)の向きは、時刻
t の位置 P における軌道の接線方向になっています。
速度
v の定義式(
( 速度 ))の右辺の極限量を、数学の「微分法」で用いられる記号で次のように表します;
lim
△t → 0 (
△r/
△t) = lim
△t → 0 {
r(
t+
△t)-
r(
t)}/
△t
≡
dr/
dt ( r の導関数 )
これを、位置ベクトル
r の時間
t に関する
導関数(
derivative )といいます。この記号を用いると、速度の定義式は
v = dr/dt (速度ベクトルを位置ベクトルの導関数で表す) 〈 式 1-2 >
と簡潔に表されます。
〇 上記の式は重要なもので、以後にも何度も用いられることを考慮して、〈 式 1-2 〉のように式に番号を付けました。
平均速度から速度を導き出す過程では、〝微小な量と微小な量の比〟の極限量を求めました。このような方法は、数学における
微分法 (
differentiation ) の考え方を応用したものです。微分法はこれと密接な関係がある
積分法 (
integration )とともに、力学で用いられる重要な数学的な方法です。
以下において、独立変数が1個である簡単な場合について、微分法と積分法の概略を説明することにします。
微分法と積分法 - 独立変数が1個であるとき -
微分法の基本的な考え方は、大まかに次のように述べることができます:
『 ある量Aが他の量Bと関数関係があるとき、〝(Aの微小変化量)/(Bの微小変化量) = (平均の変化率) 〟 を考え、(Bの微小変化量) が無限小に移行したときに (平均の変化率) が到達する (変化率) を求める 』
もう一方の積分法の基本的な考え方は、大まかに次のように述べることができます:
『 ある量Aが他の量Bと関数関係があるとき、〝 (Bの平均量) × (Aの微小変化量) を全ての (A の微小変化量) について加算した量 = (概算の総量)〟を考え、各々の (A の微小変化量) が無限小量に移行したときに (概算の総量) が到達する(総量)を求める 』
この章(
)に現れる力学的変数は、時間
t 、位置ベクトル
r、速度ベクトル
vなどであり、独立変数は
t で 従属変数は
r、
v などです。
章が進むとともに、独立変数として時間だけでなく、もっと多くの独立変数が用いられます。独立変数が複数あるときの微分・積分法の説明は、必要に応じて折々に行うことにします。
以下では、独立変数の数が1個であり、その変化を一定方向に延びる軸上の座標点として表すことができる簡単な場合について、微分法および積分法の概略を説明します。
多くの数学の教科書や参考書で用いられる例に従って、独立変数を
x とし、従属変数を
y と記します。また、
y を
x の関数として
y(
x)
のように表します。
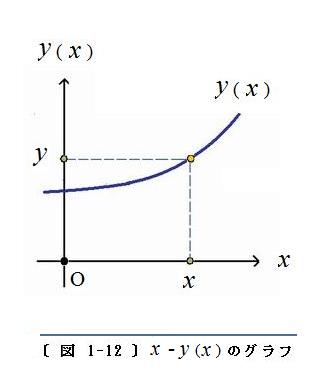
〔 図 1-12 〕 に示すように、平面上に 原点O を通り互いに直交する
x軸 と
y軸 をとります。横軸の上に一つの点
x に与えると、それに応じて縦軸の上に
y の値が定められます。
x を連続的に変化させると、
x -
y(
x) のグラフが曲線(
〔 図 〕の青色の太い線)として描かれます。
(1)平均変化率と微分係数
〔 図 1-12 〕に示す
x 軸の上に、微小な距離だけ離れた二つの点
xC と 点
xD をとり、これらの点に対する
y の値を
yC =
y(
xC) および
yD =
y(
xD) とします。ここで
xD-
xC =
△x,
yD-
yC =
△y
とすると、区間
△x の大きさは微小で、
△y の大きさも微小量になります。二つの比;
△y/
△x (平均変化率)
は、
x が区間
△x で変化するとき、それに応じて
y が変化する割合を示します。これを「平均変化率」といいます。
上記の
(平均変化率)の式で、
xC をそのままにして
xD を限りなく
xC に近づけます。すると分母の
△x は限りなくゼロに近づき、また分子の
△y も限りなくゼロに近づきます。この極限で平均変化率
△y/
△x がある値に収束すると仮定し、それを
lim △x → 0 ( △y/△x ) = {dy/dx }C (微分係数)
と表し、
y の
xC における「微分係数( differential coefficient )」といいます。
x - y(x) のグラフを用いてこの極限操作を追跡すると、微分係数 {
dy/
dx }
C は 点
xC における〝曲線
y(
x)の接線の勾配〟 に等しくなることが了解されます。
平均変化率 および 微分係数のもう少し詳しい説明を、
《 平均変化率と微分係数 》 に示します。
(微分係数) の定義式では
xC を特定の値としましたが、その代わりに、それを変数の
x に置き換えてみます。すると、微分係数は変数
x の関数とみなされます。これを
y の 「導関数( derivative )」といいます。すなわち
lim △x → 0 ( △y/△x ) = dy/dx (導関数)
となります。
〇 導関数を微分係数と同じ記号で表すなら {dy/dx }x となりますが、通常は添字の x は表示せず、単に dy/dx と表します。
〇 x の関数 y(x) が与えられているとき、導関数 dy/dx を求めることを、〝 y を x で微分する 〟などといいます。
導関数に関する公式としてよく利用されるものを
《 導関数に関する公式 》 に示します。また簡単な関数の導関数の例を
《 簡単な関数の導関数 》 に示します。
(3)面積 および 定積分
〔 図 1-12 〕に示す
x 軸上に 二つの値
xA と
xB をとり、
xA に対する
y の値を
yA =
y(
xA)、
xB に対する
y の値を
yB =
y(
xB) とします。座標 (
xA,
yA ) と 座標 (
xB,
yB ) で示される二つの点は、
x-
y(
x) の曲線上の A と B であるとします。
x-
y 平面において 四つの点〝A
xAxBB で囲まれた領域〟の面積
SAB を得るために、初めに、次のような手順でその近似的な面積
SAB ( app ) を計算します(
〝app〟は〝approximate〟の略字で、〝 近似する〟 を意味します)。
◇ xA から xB までの区間を M 個に分割し、分割点の x座標 に xk ( k = 1,2,…,M,M+1 ) のように番号を付けます(ただし、x1 = xA、xM+1 = xB)。また、これら分割点に対する y の値を yk ( k = 1,2,…,M,M+1 ) とします。ここに M は自然数です。
◇ 変数 x が区間 △xk = xk+1-xk のなかで変化すると、それに応じて y の値も変化しますが、そのときの y の平均値を yk ( mean ) と表します。
◇ 積の yk( mean ) △xk を xA から xB の間のすべての区間について加え合わせた量は、区間ABの面積 を近似したものになります。これを SAB ( app ) と記すと
SAB (app) = ∑k=1M yk ( mean )△xk ( 区間ABの面積の近似値 )
となります( 注 1-7 )。
上記の式 (
区間ABの面積の近似値 ) において、M を無限大( +∞ )の極限に移行させたとき、右辺の和はある値に収束するものと仮定します。その値を
∫xAxB y(x) dx ( xA から xB までの定積分 )
と記し、これを『 関数
y(
x) を
x について
xA から
xB まで積分する』といいます。
◇ 関数 y(x) を「被積分関数」、xA を「積分の下端」、xB を「積分の上端」といいます。
積分の下端と上端が定数である積分は、「 定積分( definite integral )」と呼ばれます。
こうして区間ABの面積
SAB は、
xA から
xB までの定積分で与えられます。すなわち
SAB = ∫xAxB y(x) dx ( 区間ABの面積 )
となります。
面積 および 定積分に関する少し詳しい解説を、
《 面積 および 定積分 》 に示します。
関数
y(
x) を、
x について下端
xA から 上端
x まで積分すると
∫
xAx y(
x)
dx
となります
( 注 1-8 )。上端の
x を任意の変数とすれば、この積分は
x の関数となります。これを
F(
x) と表せば
F(
x) = ∫
xAx y(
x)
dx (
積分関数 )
となります。
F(
x) は「積分関数」と呼ばれます。
積分の加算性を用いると、積分関数
F(
x) の
x に関する導関数は、被積分関数
y(
x) に等しくなることが示されます。すなわち
dF(x)/dx = y(x) ( 積分関数の導関数 )
となります。
上式において関数
y(
x) が与えられたとき、この式を満たす
F(
x) は一通りには決まりません。なぜなら
F(
x) に任意の定数を加えても、その導関数は同じになるからです。そのような関数を総称して、「原始関数」といいます。原子関数は、積分関数と同じ
F(
x) で表すのが通例です。したがって、原子関数の導関数についても
dF(
x)/
dx =
y(
x) (
原子関数の導関数 )
となります。
原始関数を積分関数と同じように表せば、∫
dx y(
x)
dx (ここに
d は任意の定数)となりますが、積分の下端の
d と上端の
x を省いて
F(x) = ∫ y(x) dx ( 不定積分 )
と表すのが慣例です。このように表した積分を、「不定積分( indefinite integral )」と呼びます。不定積分は、上記の (
原子関数の導関数 ) とは逆演算の関係になっています。
関数
y(
x) の原始関数
F(
x) が見出されたとします。このとき、
xA から
xB までの
y(
x) の定積分は、
x に
xB を代入した原子関数から
xA を代入した原始関数を差し引いた値に等しくなることが導かれます。すなわち
∫xAxB y(x) dx = F(xB) - F(xA) ( 微分積分法の基本公式 )
が成立します。これは「微分積分法の基本公式」と呼ばれています。
積分関数、原始関数、不定積分、微分積分法の基本公式などについて、もう少し詳しい説明を
《 不定積分 および 微分積分法の基本公式 》 に示します。
以上で説明した微分法と積分法では、初めに独立変数
x の微小量
△x をとり、最終的にそれをゼロに移行させる極限操作を行いました。
微分係数(
あるいは導関数)を求める過程をふり返ると
* 独立変数 の微小量 △x に対応する従属変数の微小量 △y を考え、その比が △x → 0 とした極限で
△y/△x → dy/dx
に収束する。
というものでした。
△x および
△y は微小量です。また
△x は微小量なので、その逆数である (1/
△x) は非常に大きな量になります。ゆえに
△y と(1/
△x)の積は、
△x をゼロと置いてしまえば、0(ゼロ)と ∞(無限大)の積になり、実数の四則演算では定義できない演算なります。
ここで
△x が限りなくゼロに近い量であるとして、これを記号の
dx で表して「無限小量」と呼ぶことにします。そうすると(1/
dx)は限りなく大きい量になり、これを「無限大量」と呼ぶことにします。
このような無限小量と無限大量を導入すると、上記の微分係数
dy/
dx は
『 無限小量 dy と 無限大量(1/dx)の積 』、または、『 無限小量 dy と 無限小量 dx の比 』
という演算として表すことができます。
一方、積分を求める過程をふり返ると
* 微小量を加算した総量を考え、それが全ての k について △xk → 0 とした極限で
∑k=1M yk ( mean )△xk → ∫xAxB y(x) dx
に収束する。
というものでした。
△xk は微小量なので、
yk ( mean )△xk も微小量です。
△xk を無限小量にすれば、和
∑k=1M における M は無限大量になります。すると 積分 ∫
xAxB y(
x)
dx は
『 無限小量 を 無限大量 の個数にわたって加え合わせる 』
という演算として表すことができます。
現在の微分積分法の観点からすれば、無限小量 や 無限大量 は、厳密に定義するのが困難です。しかしながら、力学では 位置、速度、加速度などの時間的な変化を扱うので、無限小量や無限大量は微分積分法における演算の過程を直感的で分かり易く理解するのにとても便利な考え方と言えます。レオンハルト・オイラー( Leonhard Euler, 1707年 - 1783年 )は 無限小量や無限大量を導入し、ニュートン以後に剛体力学、弾性体力学、流体力学などの発展に重要な役割を果たしました(
《 参考資料 1-5 》)。
( 注 1-7 )N 個の項 A1、A2、… 、AN を加え合わせる記号として
A1 + A2 + … + AN ≡ ∑i=1N Ai
を用いました。
( 注 1-8 )( 積分関数と被積分関数の関係 ) において、積分の上端に示す変数 x は、積分変数と同じ文字が用いられています。二つの変数を別の文字にして、例えば
∫xAx y(t) dt
のように表すこともあります。この方が丁寧な表し方ですが、混乱が生じる恐れがない限り、通常は二つを同じ文字で表します。
加速度
速度
v を時間
t の関数とし求める方法を述べましたので、次に加速度を求める方法を説明します。
〈物体を代表する点〉は、時刻
t で位置ベクトル
r(
t)で示される P におり、速度ベクトル
v(
t)の速度を有しています。時刻
t から 時刻
t+
△t までの間に〈物体を代表する点〉は軌道に沿って進み、時刻
t+
△t では位置ベクトル
r(
t+
△t)で示される 点Q に到達し、速度ベクトル
v(
t+
△t)の速度に達します。これらを
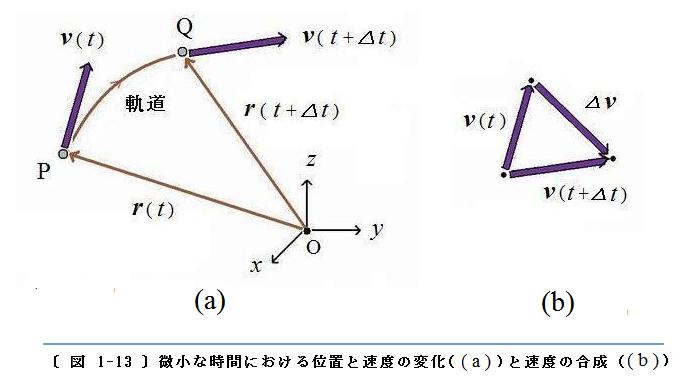
〔 図 1-13 〕 の左図( a )に示します。
v(
t)の向きは 位置 P における軌道の接線方向になり、
v(
t+
△t)の向きは 位置 Q における軌道の接線方向になります。
時刻
t から時刻
t +
△t までの間に、速度は
v(
t)から
v(
t+
△t)まで変化します。ゆえに時間間隔
△t の間に速度が変化する量は、代数式で
△v =
v(
t +
△t)-
v(
t)
( 時間間隔 △t の間に速度が変化する量 )
と表されます。この式は、-
v(
t)を左辺に移行して
v(
t)+
△v =
v(
t +
△t)
と書き直すことができます。
上記の代数式を、
〔 図 1-13 〕 の( b )に示すように、平面上の図形として描いてみます:
◇ 〔 図 1-13 〕( a )のベクトル v(t)および v(t +△t)を平行移動して、〔 図 1-13 〕( b )の平面上に移します。二つのベクトルの始点を平面上の一つの点(黒丸) に揃える(そろえる)と、〔 図 1-13 〕( b )に示すようになります。
◇ 〔 図 1-13 〕( b )において、v(t) の終点を始点として v(t +△t)の終点に向けてベクトルを描くと、それが △v になります。
代数式で表示される
△v は、このように図形として表示することができます。
△v を
△t で割った量を
a mean =
△v/
△t ={
v(
t +
△t)-
v(
t)}/
△t ( 平均加速度 )
と表し、これを 時刻
t から時刻
t+
△t までの「平均加速度」といいます。
この式(
( 平均加速度 ))で
△t の大きさを小さくしてゆき、最終的に 0(
ゼロ )に移行させた極限ではどうなるでしょうか。〔 図 1-13 〕の( a )と( b )を見較べながら調べてみます。
◇ 〔 図 1-13 〕の( a )で P の位置 r(t )と速度 v(t )はそのままにして、Q の位置を軌道に沿って P に近づけます。すると v(t +△t)は、次第に v(t)に近いベクトルになってゆきます。
◇ 〔 図 1-13 〕の( b )で v(t +△t)が v(t)に近づくと、二つのベクトルがなす角は非常に小さくなってゆくので、△v の大きさは非常に小さくなります。
◇ △t → 0 とした極限では、平均加速度 △v/△t はある大きさに収束し、その向きはある方向に収束するものと仮定します。
このように
△t → 0 の極限で、
△v/
△t は ある大きさと方向を持つベクトルの
a に収束します。これを
加速度(
acceleration )といいます。すなわち
a = lim △t → 0 ( △v/△t) = lim △t → 0 { v(t+△t)- v(t)}/△t ( 加速度 )
です。
この定義式によれば
a は時刻
t における加速度であり、これを明示したいときには
a(
t)と表します。加速度
a は、時間
t に関する速度
v の導関数として表されます。すなわち
a = dv/dt (加速度ベクトルを速度ベクトルの導関数で表す) 〈 式 1-3 〉
となります。
〇 上記の式は重要なもので、以後にも何度も用いられることを考慮して、〈 式 1-3 〉のように式に番号を付けました。
加速度は 〝 {速度}/{時間}〟の単位で表され、 国際単位系(SI)を用いいると、その単位は
[ m/s
2 ]
( 加速度の単位 )
です。
位置、速度、加速度の関係
時間とともに空間を移動する点である〈物体を代表する点〉の運動を表す方法として、位置ベクトル
r、速度ベクトル
v、および 加速度ベクトル
a を導入しました。
位置、速度、加速度ベクトルは時間
t の関数であり、位置ベクトルの時間に関する導関数は速度ベクトル;
v = dr/dt (位置ベクトルと速度ベクトルの関係)(再掲) 〈 式 1-2 >
に等しく、速度ベクトルの時間に関する導関数は加速度ベクトル;
a = dv/dt (速度ベクトルと加速度ベクトルの関係)(再掲) 〈 式 1-3 〉
に等しくなります。
加速度ベクトルは、直接に位置ベクトルを用いて表すことができます。 〈 式 1-2 〉を〈 式 1-3 〉に代入すると
a = d 2r/dt 2 (位置ベクトルと加速度ベクトルの関係)
となります。
◇ 上式の右辺の記号は、r を時間 t に関して2度にわたって微分することを表します。すなわち
d 2r/dt 2 ≡ (d/dt) ( dr /dt)
です。これを 〝 r の t に関する2階の導関数〟 といいます。
〈物体を代表する点〉の運動を図に表す -その3-
空間を移動する点の運動を表す 位置ベクトル、速度ベクトル、加速度ベクトルが得られたので、これらを用いて〈物体を代表する点〉の運動を図に表すことができます。
前ページの〔 図 1-8c 〕(
の 〈物体を代表する点〉の運動を図に表す -その2- ) に、位置ベクトル
r (
t) の時間
t を連続的に変化させ、そのときに得られる〈物体を代表する点〉の描く軌道を示すとともに、初めの時刻
ts と 終わりの時刻
t における位置ベクトル
r (
ts) と
r (
ts) (
茶色の矢印付きの線分) も併せて示しました。
ここで〔 図 1-8c 〕に追加して、時刻
ts と 時刻
t における速度ベクトル
v (
ts) と
v (
t) (
紫色の矢印付きの線分)、および、加速度ベクトル
a (
ts) と
a (
t) (
ピンク色の矢印付きの線分) を書き入れると、
〔 図 1-8c 〕 のようになります。
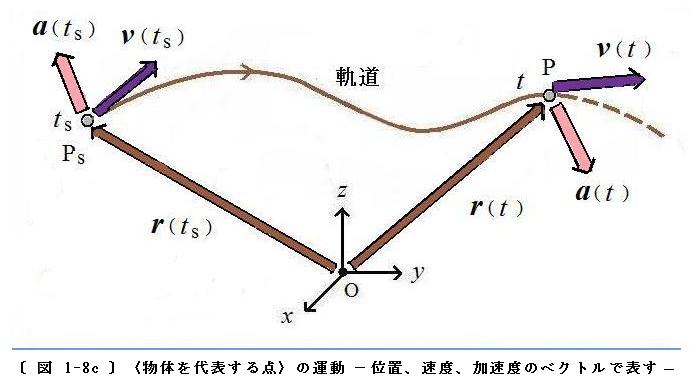
〔 図 1-8c 〕が描かれる過程を改めて述べれば、次のようになります:
◇ 直交座標系( Oxyz )の 原点O を始点にして、位置ベクトル r(t) の終点の位置を時間 t とともに追跡します。その位置は空間で曲線を描き、〔 図 1-8c 〕に示すような〈物体を代表する点〉の軌道になります。
◇ 位置ベクトル r(t) が時間 t の関数として与えられているならば、導関数 dr/dt は軌道上の全ての位置で求めることができます。〈 式 1-2 > から、これが〈物体を代表する点〉の速度ベクトル v(t) になります。
◇ 速度ベクトル v(t) が得られたら、その導関数 dv/dt は軌道上の全ての位置で求めることができます。〈 式 1-3 > から、これが〈物体を代表する点〉の加速度ベクトル a(t) になります。
図が込み入ることを避けるために、〔 図 1-8c 〕では 初めの時刻
ts と 終わりの時刻
t における 位置ベクトル、速度ベクトル、加速度ベクトル だけを書き入れました。当然のことですが、これらのベクトルは
ts から
t の間の任意の時刻に存在し、軌道上の全ての位置において描くことができます。
位置、速度、加速度に関するベクトルと座標成分の関係
力学量のベクトルを一般に
A と表し、直交座標系( O
x y z )における
x軸、
y軸、
z軸 の座標成分を
Ax、
Ay、
Az とすれば、両者は次の関係で結ばれます:
A = Axi + Ayj + Azk 〈 式 1-1 〉(再掲)
ここに、
i、
j、
k は直交座標系の基本ベクトルです(
の ベクトルと座標成分の関係 を参照 )。
ベクトル
A を位置ベクトル
r に選ぶと、〈 式 1-1 〉は
r = xi + yj + zk (位置ベクトルと座標成分の関係 )
となります。同様にして、ベクトル
A を速度ベクトル
v に選ぶと、〈 式 1-1 〉は
v = vx i + vy j + vz k (速度ベクトルと座標成分の関係 )
と表され、ベクトル
A を加速度ベクトル
a に選ぶと、〈 式 1-1 〉は
a = ax i + ay j + az k (加速度ベクトルと座標成分の関係 )
と表されます。
速度の座標成分は、〈 式 1-2 〉の関係式
v =
dr/
dt を用いると、位置の座標成分の導関数に関係づけられて
vx = dx/dt, vy = dy/dt, vz = dz/dt
(速度の座標成分と位置の座標成分の関係 )
となります。同様に加速度ベクトルの座標成分は、〈 式 1-3 〉の関係式
a =
dv/
dt を用いると、速度の座標成分の導関数に関係づけられて
ax = dvx/dt, ay = dvy/dt, az = dvz/dt
(加速度の座標成分と速度の座標成分の関係 )
となります。上記の二つの式を結び付けると
ax = d 2x/dt 2, ay = d 2y/dt 2, az = d 2z/dt 2
(加速度の座標成分と位置の座標成分の関係 )
となります。
直交座標系では、ベクトルの関係式〈 式 1-2 〉と〈 式 1-3 〉と〝 同じ形〟 の式が 座標成分の間の関係式 として得られます。そうなる理由は、基本ベクトル
i、
j、
k が時間に無関係な量であるからです。
直交座標系でない他の座標系、例えば で紹介した円柱座標系 や 球面座標系 (
《 円柱座標系 と 球座標系 -その1- 》) では、このような簡明な関係は得られません。それについては、
《 円柱座標系 と 球座標系 -その2- 》 で説明します。
位置、速度、加速度の簡単な例
この章の最後に、〈物体を代表する点〉の位置ベクトルが時間に関して簡単な関数で表される例をいくつかとり上げ、速度と加速度を求めて、その運動の有様を見てみます。
〇 すでに述べたように、〈物体を代表する点〉の位置ベクトルを時間 t の関数として r (t) と表すと、速度ベクトル v(t) と加速度ベクトル a(t) は、〈 式 1-2 〉と〈 式 1-3 〉を用いて算出されます。すなわち
v = dr/dt, a = dv/dt 〈 式 1-2 〉,〈 式 1-3 〉(再掲)
〇 なお、初めの時刻を ts = 0 とします。
(例イ)〈物体を代表する点〉が 空間の一つの点に止まり続ける運動:
空間の一つの点を Ps とし、それを位置ベクトルの r s で表すことにすれば、位置ベクトルは t ≧ 0 において
r (t) = r s
と表されます。r s は時間に無関係な一定のベクトルなので、〈 式 1-2 〉と〈 式 1-3 〉から
v(t) = 0, a(t) = 0
となります。
(例ロ)〈物体を代表する点〉が 一つの直線に沿って進む運動:
一つの直線を
f とします。直線
f は空間の点 P
s を通り、単位ベクトル
ef が示す方向に延びているとします。〈物体を代表する点〉は、
t = 0 で P
s の位置から出発し、直線に沿って進みます。位置ベクトルは
t ≧ 0 において
r (
t) =
r s +
h(
t)
ef
と表されます。ここに
h(
t) は時間
t の任意の関数で、
h(0) = 0 とします。上式に〈 式 1-2 〉と〈 式 1-3 〉を適用すると、単位ベクトル
ef は一定の方向なので
v(
t) = {
dh(
t) /
dt }
ef,
a(
t) = {
d2h(
t) /
dt2 }
ef
となります。
関数
h(
t) を具体的に指定すば 〈物体を代表する点〉の運動が定まります。次の三つのケースを挙げてみます:
・ (ケース1):
h(
t) が
t の一次式;
h(
t) =
v0t (
v0 は定数)
・ (ケース2):
h(
t) が
t の二次式;
h(
t) = (
a0/2)
t 2 (
a0 は定数)
・ (ケース3):
h(
t) が 正弦関数;
h(
t) =
h0 sin (
ω0t) (
h0、
ω0 は定数)
これらのケースにおいて、位置、速度、加速度ベクトルは次のようになります:
◇ (ケース1)では、
dh(
t) /
dt =
v0、および、
d2h(
t) /
dt2 = 0 なので
r (
t) =
r s + (
v0t )
ef
v(
t) =
v0 ef,
a(
t) = 0
となります。〈物体を代表する点〉は、直線
f に沿って一定の速度
v0ef で進みます。これを「等速直線運動」といいます。
◇ (ケース2)では、
dh(
t) /
dt =
a0t、および、
d2h(
t) /
dt2 =
a0 なので
r (
t) =
r s + { (
a0/2)
t 2 }
ef,
v(
t) = (
a0t)
ef,
a(
t) =
a0
となります。〈物体を代表する点〉は、直線
f に沿って一定の加速度
a0ef で進みます。これは、「等加速度の直線運動」になります。
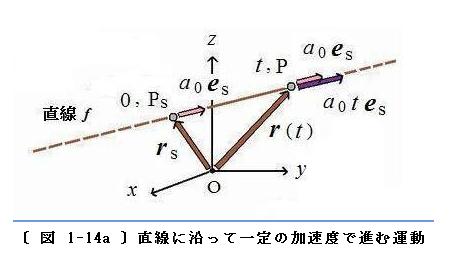
(ケース2) における〈物体を代表する点〉の軌道、および、位置、速度、加速度ベクトルを
〔 図 1-14a 〕 に示します。図には加速度の大きさ
a0 が〝正〟である場合を示しました。
〈物体を代表する点〉は
t = 0 で P
s の位置から速度ゼロで出発し、直線
f に沿って一定の大きさの加速度
a0 で進みます。速度の大きさは時間に比例して増加し、距離は時間の2乗に比例して大きくなり、時刻
t には 位置 P に達します。
a0 が負の場合には、P
s の位置から出発し、
a0 > 0 の場合とは反対の向きに進みます。
◇ (ケース3)では、
dh(
t) /
dt =
h0ω0 cos (
ω0t)、
d2h(
t) /
dt2 = -
h0ω02 sin (
ω0t)
なので
r (
t) =
r s + {
h0 sin (
ω0t) }
ef,
v(
t) = {
h0ω0 cos (
ω0t) }
ef,
a(
t) = -
h0ω02 sin (
ω0t)
ef
となります。正弦関数と余弦関数は、変数
t とともに 周期
T0 = 2π/
ω0 で周期的に変わる「周期関数」です。ゆえに〈物体を代表する点〉の位置、速度、加速度は、時間とともに 一定の周期
T0 で周期的に変化することが分かります。
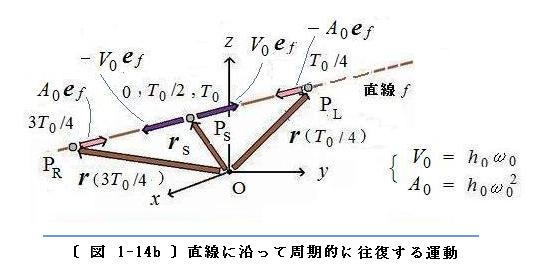 〔 図 1-14b 〕
〔 図 1-14b 〕 に、(ケース3) における〈物体を代表する点〉の軌道、および、1 周期 にわたる位置、速度、加速度ベクトルの変動を示します。図には
h0 > 0 の場合を示します。
t = 0 で〈物体を代表する点〉は P
s の位置から出発し、1/4 周期後 に直線
f の上の P
L の位置に来ます。速度の向きは
ef と同じ方向で、大きさは
h0ω0 から単調に減少して、P
L ではゼロになります。加速度の向きは
ef と反対の方向で、大きさは 0 から単調に増加して、P
L では
h0ω02 になります。1/4 周期 から 1/2 周期までは、P
L から P
s に向けて反対の向きに進みます。速度の大きさは 0 から単調に増加して
h0ω0 に達し、加速度の大きさは
h0ω02 から単調に減少し 0 になります。1/2 周期 から 3/4 周期までは P
s から直線の上の P
R に行き、3/4 周期 から 1 周期 までは P
R から出発の位置 P
s に到着します。速度と加速度の大きさは
t = 0 から 1 周期 までの場合と同じように変動しますが、それらの方向はちょうど反対の向きになっています。
図に示した 1周期 にわたる運動は、周期
T0 ごとに繰り返されます。
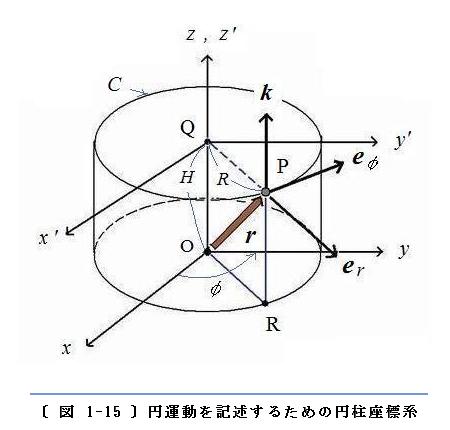
〈物体を代表する点〉が 平面上の円周に沿って進む運動:
ある一つの平面上において、〈物体を代表する点〉が半径
R の 円
C の周に沿って運動する場合を考えます。この運動を、簡単に〝円運動〟と呼ぶことにします。
この平面は、直交座標系( O
xyz )で
z =
H とした面であるとします。平面と
z 軸の 交点Q を通り、
x 軸、
y 軸、
z 軸 に平行な軸を、それぞれ、
x’ 軸、
y’ 軸、
z’ 軸 とします。半径が
R で高さが
H の円柱を
z = 0 の面に乗せれば、円柱の上面には 点Q を中心とする 半径
R の 円
C が作られます。
円
C の周に沿って回る〈物体を代表する点〉の運動を、円柱座標系(
《 円柱座標系 と 球座標系 -その1- 》 を参照)の座標成分
r、
φ、
z を用いて表します。これら3個の座標成分のうち、
φ は
x’ 軸から円周に沿って回る角度になり、残る二つの座標成分は
r =
R および
z =
H という一定の値になります。
〔 図 1-15 〕 に、直交座標系を基準にして設定した円柱座標系を示します。
時刻
t において、〈物体を代表する点〉は円周上の 点P にいるとします。Q から P の方向を向く単位ベクトルを
er 、P において 円
C の接線方向を向く単位ベクトルを
eφ、
z 軸に沿う上向きの単位ベクトルを
k とすれば、これらは互いに直交するベクトルになります。これらの単位ベクトルは、〔 図 1-15 〕に示した円柱座標系の基本ベクトルになります。
時刻
t における〈物体を代表する点〉の位置ベクトル
r (
t) は、座標成分と基本ベクトルを用いて
r (
t) =
Hk +
R er
と表されます。この式に〈 式 1-2 〉と〈 式 1-3 〉を適用します。
H、
R、
k は時間に無関係な量であり、また、
de r/
dt = (
dφ/
dt)
e φ 、
de φ/
dt = - (
dφ/
dt)
e r(
《 円柱座標系 と 球座標系 -その2- 》 を参照)となることを考慮すれば
v (
t) =
R {
dφ/
dt}
eφ
a (
t) =
R {
d2φ/
dt 2 }
eφ -
R {
dφ/
dt}
2 er
が得られます。
dφ/
dt ≡
ω と置くと、上式は簡潔に表されて
v (
t) =
Rω er
a (
t) =
R (
dω/
dt )
eφ -
Rω 2 er
と表されます。ここに
ω は、Q の周りを回る〈物体を代表する点〉の「角速度」です。
〇 角速度はベクトルとして表される力学量で、これについては後の章で改めて説明します。
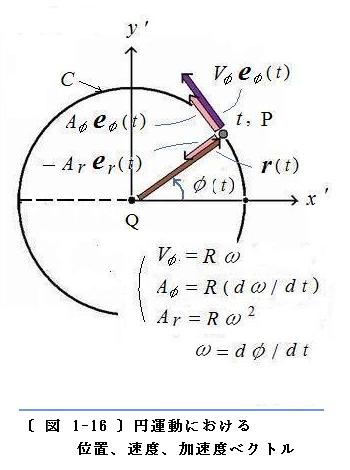 〔 図 1-16 〕
〔 図 1-16 〕 に、円周に沿って運動する〈物体を代表する点〉の 時刻
t における位置ベクトル、速度ベクトル、加速度ベクトル を(
茶色、紫色、ピンク色)で示します。
速度は P における 円
C の接線方向を向いており、その大きさは
Vφ =
Rω
です。加速度は二つの項の和になっています。一つは円の接線方向を向き大きさが
Aφ =
R (
dω/
dt)
の「接線加速度」の項で、もう一つは円の中心方向を向き大きさが
Ar =
Rω 2
の「向心加速度」の項です。
φ が 時間
t の関数として与えられれば、〈物体を代表する点〉の運動は確定されます。簡単な関数として、次のものをとり上げます。
〇 φ が時間とともに単調に増加し続けるとします。このとき、〈物体を代表する点〉は円周にそって同じ方向に回り続ける運動、すなわち〝回転運動〟を行います。φ が時間とともに単調に減少し続ける場合も同様です。ただし、そのときは回る方向が逆になります。
〇 φ がある時間のあいだは増加し、続くある時間のあいだは減少し、これを幾度も繰り返すとします。このとき、〈物体を代表する点〉は円周に沿って行ったり来たりする運動、すなわち〝往復運動〟を行います。
特に〈物体を代表する点〉が円周にそって同じ方向に等速度で回り続ける回転運動は、「等速円運動」と呼ばれます。速度の大きさを
Vφ0、角速度を
ω0 とすれば
Vφ0 =
R ω0
となります。また接線加速度の大きさを
Aφ0、向心加速度の大きさを
Ar0 とすれば
Aφ0 = 0,
Ar0 =
R ω0 2
となります。
<点> が螺旋(
らせん)軌道を描いて上昇する運動:
(例ハ)では、円柱座標系の座標成分のうち
r と
z を一定値の
R と
H に固定しました。ここで
r=
R としたままで
z を変化させると、〈物体を代表する点〉は円軌道を描きながら
z軸 の方向に進む運動、いわゆる〝螺旋(
らせん)〟の軌道を描いて上昇する運動を行います。円柱座標系を用いてこの運動を調べてみましょう。
簡単のため、〈物体を代表する点〉は
z 軸 方向に一定の速さ
Vz0 で進み、
z 軸に垂直な平面(
x-
y 平面 )上を回る運動は等速円運動であるとします。等速円運動をするときの速度の大きさを
Vφ0、角速度の大きさを
ω0、周期を
T0 = 2π/
ω0 とすると、〈物体を代表する点〉の 位置ベクトル
r (
t)、速度ベクトル
v (
t) 、加速度ベクトル
a (
t) は、それぞれ
r (
t) = (
H +
Vz0t )
k +
R er
v (
t) =
Vz0k +
Rω0eφ
a (
t) = -
Rω0 2er
となります。基本ベクトルの
k は時間に無関係な一定のベクトルですが、基本ベクトルの
er と
eφ は時間とともに変化します。
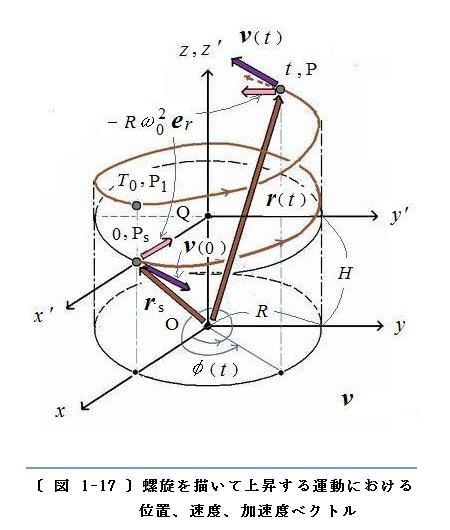
〈物体を代表する点〉の速度は、円軌道の接線方向を向く速度
Rω0eφ と
z 軸方向を向く速度
Vz0k を加え合わせたものです。加速度は、
z 軸に垂直な平面(
x-
y 平面 )において〈物体を代表する点〉の位置から
z 軸に垂線を下ろした方向を向きます。
〔 図 1-17 〕 に、〈物体を代表する点〉が描く軌道、および、位置、速度、加速度ベクトル を示します。〔 図 〕には、初めの時刻 0 で
z =
H、
φ = 0 の位置 P
s から出発し、
z 軸 の周りを1回転して時刻
T0 で位置 P
1 に、1周期と2周期のあいだの時刻
t で 位置 P に到るまでの軌道(
茶色の太い曲線) 、および、時刻 0、時刻
T0、時刻
t における位置、速度、加速度ベクトル(
茶色、紫色、ピンク色)が描いてあります。〈物体を代表する点〉の速度
v は
Rω0eφ と
Vz0k を加え合わせたものですが、いつも軌道上における接線方向を向きます。
以上の (例イ)、(例ロ)、(例ハ)、(例ニ) に示した例は、いずれも〈物体を代表する点〉の位置ベクトルを簡単な時間に関する関数
r (
t) で表したとき、その速度ベクトル
v(
t) や 加速度ベクトル
a(
t) がどのように表されるかを示したものです。位置、速度、加速度をベクトルで表すと、〈物体を代表する点〉の軌道、および、位置、速度、加速度は非常に分かり易く図に表示できることが分かります。
当然ながら、実際の運動はこのような単純なものでなく、位置ベクトルは任意の関数として表されます。その場合でも、例に示したような簡単な関数で表した運動は、実際の運動の概略を理解したり近似したりするのに非常に役に立ちます。
◇ 《 参考資料 1-5 》
高瀬正仁著、「無限解析のはじまり- 私のオイラー -」、ちくま学芸文庫、2009年発行。
《 改定 第1章 ―第3ステップ― 》では、〈物体を代表する点〉の 位置ベクトル が与えられているとき、微分法を用いて〈物体を代表する点〉 の 速度ベクトル と 加速度ベクトル を導きました。その概要は次のようです:
速度ベクトルは 位置ベクトル の時間に関する導関数で表され、加速度ベクトル は 速度ベクトル の時間に関する導関数で表されます。位置、速度、加速度などの力学量をベクトルで表したとき、ベクトルの力学量は力学量の座標と 1対1 に対応します。この章の終りに、位置ベクトルが時間の簡単な関数として表される例を挙げ、そのときの 速度ベクトルと加速度ベクトル を示しました。
≪ 改定 第1章 終了 ≫
<
このページの
トッップヘ
 〔 図 1-10 〕 に示すように、時刻 t から微小時間 △t 経過した t + △t までの間に〈物体を代表する点〉が軌道に沿って空間の 点P から Q の位置に移動したとします。
〔 図 1-10 〕 に示すように、時刻 t から微小時間 △t 経過した t + △t までの間に〈物体を代表する点〉が軌道に沿って空間の 点P から Q の位置に移動したとします。 速度の定義から明らかなように、△t → 0 の極限で得られる v は、時刻 t における速度であることが分かります。時刻の t は任意の時間に選べるので、v は時間 t の関数と見なすことができます。これを明示すれば
速度の定義から明らかなように、△t → 0 の極限で得られる v は、時刻 t における速度であることが分かります。時刻の t は任意の時間に選べるので、v は時間 t の関数と見なすことができます。これを明示すれば この章(
この章(

 (ケース2) における〈物体を代表する点〉の軌道、および、位置、速度、加速度ベクトルを
(ケース2) における〈物体を代表する点〉の軌道、および、位置、速度、加速度ベクトルを 
 時刻 t において、〈物体を代表する点〉は円周上の 点P にいるとします。Q から P の方向を向く単位ベクトルを er 、P において 円C の接線方向を向く単位ベクトルを eφ、z 軸に沿う上向きの単位ベクトルを k とすれば、これらは互いに直交するベクトルになります。これらの単位ベクトルは、〔 図 1-15 〕に示した円柱座標系の基本ベクトルになります。
時刻 t において、〈物体を代表する点〉は円周上の 点P にいるとします。Q から P の方向を向く単位ベクトルを er 、P において 円C の接線方向を向く単位ベクトルを eφ、z 軸に沿う上向きの単位ベクトルを k とすれば、これらは互いに直交するベクトルになります。これらの単位ベクトルは、〔 図 1-15 〕に示した円柱座標系の基本ベクトルになります。
 〈物体を代表する点〉の速度は、円軌道の接線方向を向く速度 Rω0eφ と z 軸方向を向く速度 Vz0k を加え合わせたものです。加速度は、z 軸に垂直な平面( x-y 平面 )において〈物体を代表する点〉の位置から z 軸に垂線を下ろした方向を向きます。
〈物体を代表する点〉の速度は、円軌道の接線方向を向く速度 Rω0eφ と z 軸方向を向く速度 Vz0k を加え合わせたものです。加速度は、z 軸に垂直な平面( x-y 平面 )において〈物体を代表する点〉の位置から z 軸に垂線を下ろした方向を向きます。