トップ
《 改定 第1章 ―第2ステップ― 》
第2ステップでは、空間の点の位置を表す方法として「位置ベクトル」を導入します。〈物体を代表する点〉の運動は、位置ベクトルを時間の関数として表すことができます。
位置ベクトルは大きさと方向を兼ね備えた量で、物理学において現れるベクトルの一つです。ベクトルを導入すると、力学量の関係を図形的に把握して、物体の運動を直感的に理解できる利点があります。ベクトルで表した力学量は、座標で表した力学量と1対1に対応します。
位置ベクトル
空間に直交座標系( O
xyz )を設定し、前のページの〔 図 1-6a 〕に示したような図形的な操作を行って、空間の一つの点Pの位置を座標 (
x,
y,
z ) で表しました(
)。点Pの位置を表す別の方法として、次のような「位置ベクトル」を用いる方法があります。
原点O から 点P に向けて線分を引き、その先端に矢印を付けます。空間に描いたこの矢印付き線分のことを、
位置ベクトル (
position vector ) といいます。
〔 図 1-6b 〕 に、位置ベクトルを茶色の矢印付きの線分で示します。

矢印付き線分の始まる点を位置ベクトルの
始点 といい、終わる点を
終点 といいます。〔 図 1-6b 〕では、原点O が始点であり、点P が終点です。点P の位置は、位置ベクトルの終点の位置でもって表わされます。
〔 図 1-6b 〕に示した位置ベクトルは、二つの量を兼ね備えた量です。その一つは
〝線分OPの長さ(
OとPの間の距離)〟
であり、もう一つは
〝線分の始点Oから終点Pを向く方向〟
です。このように『 大きさと方向を兼ね備えた量 』のことを一般に
ベクトル (
vector ) と呼びます。
◇ これ以後にも、いろいろなベクトルが登場します。ここに述べた位置ベクトルは、そのなかの一つになります。
矢印付き線分として図に描いた位置ベクトルを、何らかの代数的な記号として表すのは便利です。通常は、二つの表記が用いられます:
◇ その一つは、位置ベクトルの始点が O で終点が P であることを明記して、OPの上に矢印(→)を付けて

と表記する方法です。
◇ もう一つは、イタリック体の
r を太字にして
r
と表記する方法です。位置ベクトルが大きさ(
長さ )だけの量なら太字にせずに通常の
r で表せば良いのですが、方向も兼ね備えた量なので、それを示す意味で太字の
r と表記するのです。
〔 図 1-6b 〕には、矢印付き線分の傍に上記の二つの代数的な記号を記しました。多くの場合に、位置ベクトルを表記するのに
r が用いられます。イタリック体を太字にしたこの表記法は、位置ベクトルに限らず、他のベクトルを表すときにもよく用いられます。このホームページでも、主としてこの表記法を用います。
位置ベクトルの単位は位置座標の単位と同じであり、 国際単位系(SI)を用いると
[ m ]
( 位置の単位 )
となります。
位置ベクトルと位置座標
空間の点Pの位置は、〔 図 1-6b 〕のように位置ベクトル
r で表されるとともに、前ページの〔 図 1-6a 〕(
)のように位置座標(
x,
y,
z )でも表されます。直交座標系( O
xyz )の空間において二つの図(
〔 図 1-6a 〕と〔 図 1-6b 〕)を重ねると、
〔 図 1-6c 〕 のようになります。
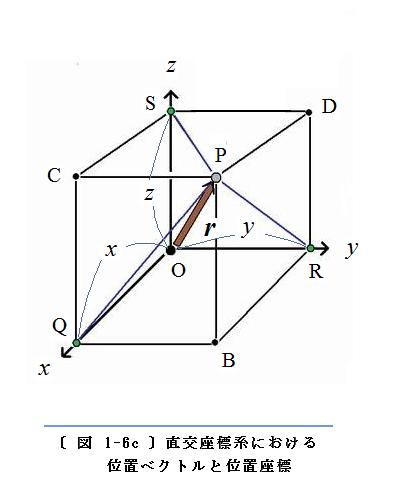
位置ベクトル
r と位置座標(
x,
y,
z )のあいだには
〝1対1〟
の関係があります。すなわち、位置ベクトルの
r を与えると 位置座標(
x,
y,
z )が一通りに定まり、位置座標の(
x,
y,
z )を与えると位置ベクトル
r が一通りに定まります。両者のこのような関係は、二つを 等号 = で結んで
r = ( x,y,z )
( 位置ベクトルと位置座標の関係 )
という式で表されます。
ニュートン力学では、位置ベクトルの他にいくつかのベクトルが用いられます。直ぐ後で述べる「変位ベクトル」、それに続いて「速度ベクトル」と「加速度ベクトル」((
)、さらには「力ベクトル」、「運動量ベクトル」(
)などが現れます。いずれも大きさと方向を兼ね備えたベクトルの力学量で、代数的な記号で
A と表すことにします。
ベクトル
A は、〔 図 1-6c 〕と同様に、直交座標系の空間に始点と終点を持つベクトルとして図示することができます。このときの座標成分を
Ax、
Ay、
Az と表せば、ベクトルと座標の関係は、上記の
(位置ベクトルと位置座標の関係) と同形の式;
A = ( Ax,Ay,Az ) ( ベクトルと座標の関係 )
で表されます。
◇ 位置ベクトル r と一般の力学量のベクトル A は、ともに直交座標系を用いて表される〝3次元空間〟で表示されます。そのとき、( 位置ベクトルと位置座標の関係 )と ( ベクトルと座標の関係 )は同形の式になります。
◇ ただし、二つのベクトルの単位は一般に異なることに注意する必要があります。位置ベクトルの単位は [ m ] ですが、例えば A が速度ベクトルであるとすれば、その単位は [ m/s ] です。位置ベクトルを表示する空間は x軸、y軸、z軸という座標軸を用いて表されますが、速度ベクトルを表示する空間は、速度の単位を持つ座標軸を用いて表されます。
〈物体を代表する点〉の運動を図に表す -その2-
前のページで導入した〈物体を代表する点〉は空間の点なので、その位置を位置ベクトルを用いて表すことができます。空間の点は時間が経過しても静止したままですが、<物体を代表する点>は時間が経過すると一般には空間を移動します。したがって、その位置は時間
t の関数になり、位置ベクトルを用いて表せば
r ( t )
となります。
初めの時刻
ts で位置ベクトルは
r (
t s ) となり、その終点は空間の点 P
s を指します。初めの時刻
ts から 時刻
t まで、時間を連続的に変化させます。位置ベクトルの終点は空間の点を次々と辿り(
たどり)、時刻
t で位置ベクトル
r (
t ) の終点は空間の点 P を指します。時間の経過とともに作られる位置ベクトルの終点を繋げる(
つなげる)と、
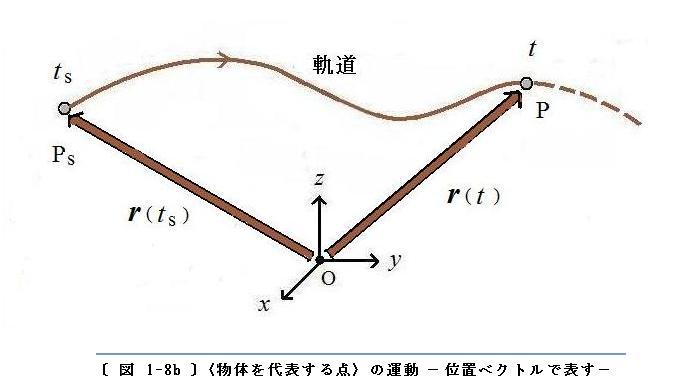
〔 図 1-8b 〕 に示すような〈物体を代表する点〉の軌道(
茶色の曲線)になります。
〔 図 1-8b 〕には、初めの時刻
ts と 終わりの時刻
t における位置ベクトル(
茶色の矢印付き線分)だけを示しました。当然ながら、途中の任意の時刻における位置ベクトルも同様に描くことができます。すべての時刻における位置ベクトルの始点は、直交座標系( O
xyz )の 原点O です。
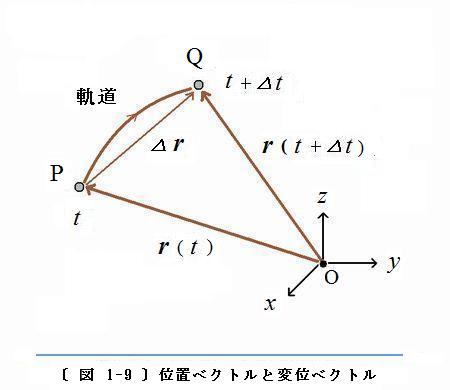
変位、および、変位ベクトル
〈物体を代表する点〉が 時刻
t で位置ベクトル
r(
t )の終点 P の位置におり、
△t だけ時間が経過する間に、位置ベクトル
r(
t +
△t )の終点 Q の位置まで移動したとします。これを
〔 図 1-9 〕 に示します。
このように、空間の点の位置が時間の経過とともに変化することを
変位 (
displacement ) といいます。
◇ △ はこの後に記す量が変化した量を示すときに用いる記号で、△t は時間変数 t が △t だけ変化したことを表します。
〔 図 1-9 〕では、〈物体を代表する点〉は 時間
△t の間に P から Q に変位しています。ここで P を始点とし Q を終点とするベクトル
△r を作って、これを
変位ベクトル (
displacement vector ) と呼びます。
◇ 時刻が t から t + △t まで経過する間に、〈物体を代表する点〉は軌道の曲線 PQ に沿って動きます。一方の変位ベクトル △r は、始点 P から終点 Q に向かうベクトルです。
次のページでは、微小な時間
△t における変位ベクトル
△r をとり上げます。その場合には、変位ベクトルは実際の軌道を近似したものになります(
)。
変位ベクトルの単位は位置ベクトルの単位と同じであり、 国際単位系(SI)を用いると
[ m ]
( 変位の単位 )
となります。
変位ベクトルは位置ベクトルと良く似たベクトルで、ともに大きさが空間の距離の単位 [ m ] で表されます。しかし、二つは用いられる目的が異なります。位置ベクトルは、点が空間の何処(
どこ )にいるかを示す目的で用いられます。そのため、位置ベクトルの始点はどの時刻でも共通に 原点O が選ばれます。これに対して変位ベクトルは、点の位置が空間でどれだけ変化したのかを示す目的で用いられます。そのため、変位する前後の位置を表す始点と終点は、一般には時間の経過とともに次々に変わります。
ベクトル および ベクトルの演算
上記の〔 図 1-9 〕で O、P、Q の三つの点を直線で結ぶと、三角形 OPQ になります。三角形のそれぞれの辺は、位置ベクトル
r(
t ) 、変位ベクトル
△r、位置ベクトル
r(
t+
△t ) から成っています。ベクトルの方向に沿って二つの経路を辿って(
たどって)みます。
(経路1);r( t ) を O から P まで辿り、続いて、△r を P から Q まで辿る。
(経路2);r( t+△t ) を O から Q まで辿る。
どちらの経路も、同じ点 O から出発し同じ点 Q に着きます。
図形的なこの関係は、位置ベクトル
r(
t ) に変位ベクトル
△r を加え合わせれば、それが位置ベクトルの
r(
t+
△t ) に等しくなるという代数式;
r( t ) + △r = r( t+△t ) (位置ベクトルと変位ベクトルの加法・減法)
に置き換えて表すことができます。
ベクトルに関する種々の関係は、この例に示したように、『 図形で表す方法 』と『 代数式で表す方法 』の二つが用いられます。図形で表す方法では、ベクトルに関する関係は図面に描いたベクトルの
図形的な操作 として表されます。代数式で表す方法では、ベクトルに関する関係は
式の演算 で表されます。
力学において、物体の運動を記述するために種々の量が用いられます。そのうち特に基本となる量として用いられるものを、
力学量(
mechanical quantity )
( 注 1-6 ) といいます。これまで登場した力学量は、時間、位置の座標、位置ベクトル、変位ベクトル などですが、これ以後にも、新たにいろいろな力学量が登場します。
力学量のうち、このページで導入した位置ベクトルや変位ベクトルは、大きさと方向を兼ね備えた量です。すでに述べたように、これらは「ベクトル」と呼ばれます。これに対して、大きさだけを持つ力学量もあります。時間、位置ベクトルの大きさ、変位ベクトルの大きさ などです。このような力学量のことを、
スカラー(
scalar )といいます。
以下の(1)-(4)において、ベクトルに関する関係をまとめて示します。なお、ベクトルを
A、
B 、
C 、スカラーを
c などで表します。ベクトルの大きさ、例えば ベクトル
A の大きさを、絶対値の記号を用いて|
A|と表します。
(1)ベクトルの加法・減法
ベクトルの加法・減法は、三つのベクトル
A、
B 、
C から任意の二つを選び、二つのベクトルの和あるいは差が三つ目のベクトルに等しくなるという演算として表されます。
ベクトル
A と
B の和は
C = A + B ( ベクトルの加法 )
と表されます。上式でベクトル
A を移行し、符号を変えれば
B = C - A ( ベクトルの減法 )
となります。
式の演算(
左辺と右辺のあいだで移項)を行うと、上記の二つの式は同一の式になります。ゆえに、これらを併せて
( ベクトルの加法・減法 ) とすることができます。
ベクトルの加法・減法の演算に対応する図形と関連する事柄について、もう少し詳しい説明を
《 ベクトルの加法・減法 》 に示します。
スカラー
c に ベクトル
A をかけて
cA (ベクトルとスカラーの積)
としたものを、「ベクトルとスカラーの積」といいます。この量はベクトルであり、その大きさと方向は次のようです:
◇ cA の方向は、A と同じ向きか、あるいは、A と反対向きである。
◇ c ={実数}[cの単位] のように表したとき、cA の方向は c > 0 なら A と同じ向きになり、 c < 0 なら、A と反対 の向きになる。
cA の単位は、〝
c の単位 と
A の単位 の積〟になります。
ベクトルとスカラーの積
cA において
c = 1 と置けば、
cA =
A となります。この式の左辺の
c に 1 =|
A|/|
A|を代入すれば
(|
A|/|
A|)
A =
A
となります。左辺は (
A/|
A|)|
A|に等しいので、これから(
左辺と右辺を入れ替えて示せば)
A =
eA|
A|
という式が得られます。ここに
eA = A/|A| ( A の単位ベクトル )
で、この量をベクトル
A の
単位ベクトル(
unit vector ) といいます。
単位ベクトル
eA の大きさは1、すなわち
|
eA|=1
であり、その方向は
A と同じ方向を向くベクトルです。単位ベクトル
eA は単位がない量なので、ベクトル
A と |
A|
eA は同じ単位になります。
任意のベクトル
A は、このように、その大きさ|
A|とその方向を示す
eA の積として表されることが分かります。これはベクトルを表すのに非常に便利です。
直交座標系( O
xyz )の座標軸の方向を向く単位ベクトルは、三つあります。すなわち、
x軸方向 を向く単位ベクトル、
y軸方向 を向く単位ベクトル、
z軸方向 を向く単位ベクトルです。これらは、次の記号;
i、j、k ( x軸方向、y軸方向、z軸方向 を向く単位ベクトル )
で表され、
基本ベクトル(
fundamental vector )と呼ばれます。
単位ベクトルおよび基本ベクトルについて、もう少し詳しい説明を
《 単位ベクトルと基本ベクトル 》 に示します。
ベクトルとベクトルをかける演算には、二種類あります。一つは演算した結果が〝スカラー〟になるもので、もう一つは演算した結果が〝ベクトル〟になるものです。前者の演算を ベクトルの
内積(
inner product )といいます(
別名で スカラー積 ( scalar product ) ともいいます )。後者の演算については、この後の(5)で説明します。
ベクトル
A とベクトル
B の内積を
A ・B (ベクトルの内積)
と表します。ベクトルの内積は、スカラー量になります。ベクトルの内積を計算する式は
A ・B =|A||B|cos θ (ベクトルの内積の計算式)
です。ここに
θ は、
A と
B の始点を揃えて(
そろえて)図面に描いたとき、二つのベクトルで挟まれる(
はさまれる)角度を表します。
◇ |A|と|B|が一定の大きさであるとき、θ をゼロから π( ラジアン )まで変化させると、内積は単調に減少し
θ = 0 のとき最大値;A ・B =|A||B|
θ = π/2 のときゼロ;A ・B = 0
θ = π のとき最小値;A ・B = -|A||B|
になります。さらに θ を π から 2π まで変化させると、内積は最小値の -|A||B|から単調に増加して、最大値の|A||B|に達します。
ベクトルの内積 および 関連する事柄について、もう少し詳しい説明を
《 ベクトルの内積 》 に示します。
ベクトルとベクトルをかける演算として、その結果がベクトルになる演算のことを、ベクトルの
外積(
outer product )といいます(
別名で ベクトル積 ( vector product ) ともいいます )。
ベクトル
A とベクトル
B の外積を
A × B (ベクトルの外積)
と表します。ベクトルの外積はベクトルであり、その方向と大きさを次のように定めます。すなわち
◇ A × B の方向は、A と B の始点を揃えて(そろえて)図面に描いたとき、A と B で作られる平面に垂直な方向。
◇ A × B の大きさは
|A × B| =|A||B|sin θ (ベクトルの外積の大きさ)
で与えられる。ここに θ は、A と B の始点を揃えて(そろえて)図面に描いたとき、二つのベクトルで挟まれる(はさまれる)角度である。
ただし、
A と
B で作られる平面に垂直な向きは、二通りあります。そこで
『 A から B に右ネジを回したとき、そのネジが進む向き 』
と定めることにします。
ベクトルの外積 および 関連する事柄について、もう少し詳しい説明を
《 ベクトルの外積 》 に示します。
( 注 1-6 )力学量( mechanical quantity )という言葉は、力学の教科書や参考書でしばしば用いられます。けれども、用語として明確に定義づけられてはいないようです。このホームページでは、「力学量」を重要な概念として何度も用いることにします。
ベクトルと座標成分の関係
これまで説明した ベクトルとベクトルの演算 は、力学量として現れるいろいろなベクトルに共通に適用されます。力学量のベクトルを一般に
A と表し、直交座標系( O
x y z )における
x軸、
y軸、
z軸 の座標成分を
Ax、
Ay、
Az とします。ベクトルとその座標成分について、三次元の空間で位置ベクトルのときに示した〔 図 1-6c 〕と同様に描けば、
〔 図 1-6d 〕 のようになります。
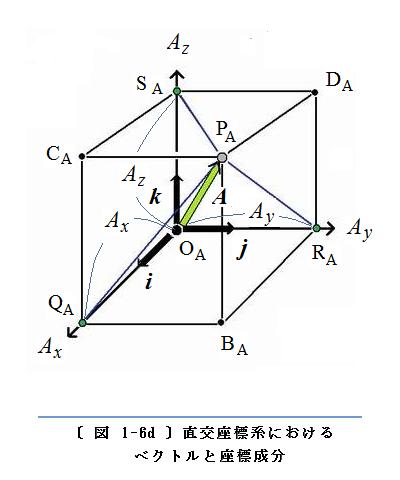
〔 図 1-6c 〕と〔 図 1-6d 〕を比較してみます。前者の座標軸は
x軸、
y軸、
z軸 であり、空間は位置の空間でになります。これに対して後者では、座標軸は
Ax軸、
Ay軸、
Az軸であり、空間は力学量の
A で表される空間になります。だたし座標軸の示す方向は、二つの図では共通であり、直交座標系における基本ベクトルの
i、
j、
k で表されます。
こうして〔 図 1-6d 〕から、ベクトル
A とその座標成分の関係は、
A = Axi + Ayj + Azk
あるいは、簡潔に
A = ( Ax,Ay,Az )
〈 式 1-1 〉
と表されます。ベクトルとその座標成分のあいだには〝1対1〟の関係があります。すなわち、ベクトルを与えると 座標成分が一通りに定まり、座標成分を与えるとベクトルが一通りに定まります。
〇 式に番号を付けることは、数学や力学などの教科書ではよく用いる方法です。ただし、番号の数が多くなると面倒で煩わしく、かえって内容が分かり難くなる傾向があります。これを考慮して、このホームページでは番号を付けた式の数をできるだけ減らすように心がけています。そこで幾度も現れる重要な式については、式の番号を上記のように括弧〈 〉で囲って、〈 式 1-1 >、 < 式 1-2 >、… のように示すことにします。なお、番号の初めの 1 は 章の番号、次の 1 は その章 の 1番目の式であることを示します。
座標成分
Ax、
Ay、
Az は、〈 式 1-1 〉において基本ベクトル
i、
j、
k の係数になっています。それぞれの基本ベクトルと〈 式 1-1 〉のベクトルの内積を作れば
Ax = A ・i = |A|cos θ x, Ay = A ・j =|A|cos θ y, Az = A ・k =|A|cos θ z
(ベクトルの座標成分、および、ベクトルと座標軸のなす角)
が得られます。ここに
θ x、
θ y、
θ z は、それぞれ、ベクトル
A と
i、
j、
k のなす角です。
〔 図 1-6d 〕と〈 式 1-1 〉に示したベクトルと座標成分の関係は、直交座標系( O
x y z )において成立するものです。これ以外の座標系、例えば円柱座標系や球座標系 (
《 円柱座標系 と 球座標系 -その1- 》) を選んだ場合には、このような簡単な関係は成立しません。それについては、次ページにおいて
《 円柱座標系 と 球座標系 -その2- 》 で説明します。
図形で表示する方法、および、代数式で表示する方法
ベクトルを用いて物体の運動を表す利点は、空間における図形的な変化を直接に追跡することにあります。現象を直感的に理解するには、身近な物体を観察して得た情報を図形で捉える(
とらえる )のが早道であると言えます。
しかしその一方で、図形的な変化を直接に追跡するのが困難なこともあります。図形が混み入りゴチャゴチャしてくると、図形の変化を正確に把握するのは難しくなります。
〇 3次元の空間の立体図形は、しばしば紙面や画面の上に投射された平面図形として表されます。2次元の平面上では、図形を扱うのが相当に簡単になります。
〇 しかし立体図形を平面図形に投影したり、あるいは、平面図形から立体図形を作り上げたりする作業には、かなりの熟練と経験が要求されます。図形が複雑に変化するときは、その作業は非常に困難になるでしょう。
代数式を活用すると、図形的な変化を追跡するときに出会う困難を大幅に緩和することができます。何故なら、式を演算する操作は定められた規則に従って行えば良いので、少し訓練すれば簡単にでき、紙面、地面、黒板 などに書きながら機械的に進められます。その過程では、図形の複雑な関係に思い悩む苦労はありません。
代数式における演算は、図形における操作と1対1に対応します。代数式の演算は、したがって、図形における一つ一つの複雑な操作を代行してくれます。これは誠にありがたいことです。
代数式はこのように非常に有用でなのすが、その利点が逆に望ましくない結果を招くこともあります。代数式を演算する操作は容易なので、代数式やその演算が図形の変化にどう対応しているかを考えることが疎かに(
おろそかに )なりがちです。
力学は物体の運動を論ずるのが目的です。代数式の演算を通してある結果が得られたときには、それが空間における物体の運動にどのように関係しているのか、という問題を絶えず吟味することが必要です。
《 改定 第1章 ―第2ステップ― 》では、〈物体を代表する点〉の運動を位置ベクトルと変位ベクトルを用いて表す方法を述べるとともに、ベクトルに関する演算、および、位置ベクトルと位置座標の関係について述べました。その概要は次のようです:
空間の点の位置を位置ベクトルで表す方法を用いると、〈物体を代表する点〉の位置の時間的な変化は、位置ベクトルに変位ベクトルを次々に加え合わてゆくベクトルの演算として表されます。空間の点の位置は、位置ベクトルまたは位置の座標で表され、両者の間には 1対1 の関係があります。
次の
では、〈物体を代表する点〉 の速度と加速度を微分法を用いて導くとともに、微分・積分法の観点から、〈物体を代表する点〉の位置、速度、加速度の関係を明らかにします。
このページの
トッップヘ
 矢印付き線分の始まる点を位置ベクトルの 始点 といい、終わる点を 終点 といいます。〔 図 1-6b 〕では、原点O が始点であり、点P が終点です。点P の位置は、位置ベクトルの終点の位置でもって表わされます。
矢印付き線分の始まる点を位置ベクトルの 始点 といい、終わる点を 終点 といいます。〔 図 1-6b 〕では、原点O が始点であり、点P が終点です。点P の位置は、位置ベクトルの終点の位置でもって表わされます。
 位置ベクトル r と位置座標( x,y,z )のあいだには
位置ベクトル r と位置座標( x,y,z )のあいだには

 〔 図 1-6c 〕と〔 図 1-6d 〕を比較してみます。前者の座標軸は x軸、y軸、z軸 であり、空間は位置の空間でになります。これに対して後者では、座標軸は Ax軸、Ay軸、Az軸であり、空間は力学量の A で表される空間になります。だたし座標軸の示す方向は、二つの図では共通であり、直交座標系における基本ベクトルの i、j、k で表されます。
〔 図 1-6c 〕と〔 図 1-6d 〕を比較してみます。前者の座標軸は x軸、y軸、z軸 であり、空間は位置の空間でになります。これに対して後者では、座標軸は Ax軸、Ay軸、Az軸であり、空間は力学量の A で表される空間になります。だたし座標軸の示す方向は、二つの図では共通であり、直交座標系における基本ベクトルの i、j、k で表されます。