トップ
《 改定 第1章 ―第1ステップ― 》
第1ステップでは、空間に在る一つの物体を<物体を代表する点> という一つの点で代表させるという簡単な方法を採用し、この点の運動を「座標系」と「座標」を用いて数量的に表す方法について説明します。
身近な風景において物体の運動を観察する
私たちの周囲の身近な風景を眺めて、どのような物体がどのように運動するのかを観察してみましょう。例として、次の三つの風景をとりあげます。

(a)部屋の中の風景
部屋の中で、人が椅子に腰かけて机の上に置かれたパソコンに向かって作業をしています。机の横の台には電気コンロが置かれ、その上にヤカンが乗せられています。天井から吊るされている蛍光灯が部屋の中を明るく照らしています。
人の右側には開け放った窓があり、外から吹き込む風でカーテンが内側になびき、ヤカンから立ち昇る湯気がゆらゆらと揺れています。机の上に置いたあったサッカーボールが人の肱と接触し、床に落下して弾みながら床の上を転がります。部屋の中のこのような風景を、
〔 図 1-1a 〕 に示します。
この風景で現れる物体を列挙してみます。
床の上に机、椅子、台があり、机の上にパソコン、台の上に電気コンロ、ヤカンが置かれ、床面ではサッカーボールが転っています。また、天井から吊るされた蛍光灯、窓に掛けられてたカーテンがあります。さらに生物ではありますが、椅子の上には座っている人がいます。
(b)野外の風景
パソコンで作業をして人が、立ち上がって窓から戸外を眺めます。

野外では、すぐ近くを高速道路が通っています。それは川を超えて遠くに立ち並ぶビルディングの方向へ伸びています。道路の脇には常緑樹の大きな樹木があり、高速道路の上を乗用車、トラック、バスなどの自動車が次々と走行してゆきます。一般道路の上には、停車していたり走行する自動車が見られます。川の水は左方にゆったりと流れ、川の上には橋が架かっています。
上空には一羽の鳥が悠然と飛行しています。遠方を眺めると、山々の上にはうっすらと雲がなびき、太陽から差す穏やかな夕日が地上を照らしています。野外のこのような風景を、
〔 図 1-1b 〕 に示します。
この風景に現れる物体を列挙してみます。
高速道路の上を走る自動車、一般道路の上では停車したり動いている自動車があります。遠方にあるビルディングや家屋、川の上に架けられた橋があります。空に浮かんだように見える太陽は、地球からずいぶん離れたところにある巨大な天体であることが知られていますが、これも物体ということができます。生物として、道路の脇にある樹木、および、空を飛んでいる鳥があります。

(c)夜空の風景
太陽が没してあたりが暗くなるにつれて、昼間に見られていた野外の風景は暗闇に覆われてゆきます。それとともに、空には星が一つ、二つと現れ始め、その数が次第に増えてゆきます。あたりがすっかり暗くなると、夜空が一面に星でちりばめられます。
星々はほとんど同じ位置に止まっているように見えます。しかし時間がだいぶ経ってから空を見上げると、星々は全体としてその位置がいくらか移動しているようです。夜空を見上げたときのこうした風景を、
〔 図 1-1c 〕 に示します。
この風景で現れる物体を列挙してみます。
夜空に浮かんだように見える数々の星がありますが、これらも太陽と同様に物体ということができます。
夜になると、昼間に見られていた多くの物体は闇の中に没して見えなくなります。もちろん、私たちはこれらの物体が消えて無くなったとは考えません。昼間と同じように存在するけれども、私たちの視覚では認識できなくなったのです。
どんなものが物体なのか
〔 図 1-1 〕に示した三つの風景では、いろいろな物体が登場します。ところで、どんなものを 〝物体〟 と言うのでしょうか? それを物体と言うのは、それがどんな条件を備えているからでしょうか? 三つの風景に現れた物体を念頭において、このことを検討してみます。
物体はそれぞれが固有の形を持っています。それは外部に対して閉じた形をしており、物体の内部と外部を分ける境界面が存在します。ゆえに物体である条件の一つは、その形か閉じており、境界面で外部と内部とに分けられていることです。
物体の内部にはいろいろな物質が詰め込まれています。机や椅子は多くが木で作られていますが、ときには金属やプラスチックで作られたり、あるいは木材と金属を組み合わせて作られることもあります。自動車は大部分が種々の金属から成りますが、さらに様々なプラスチック類や布類が使われ、燃料としてガソリンなどの液体燃料が使われたりします。このように物体は、固体、液体、気体など種々の相として多種多様の物質から作り上げられています。ゆえに物体である他の条件は、その内部が何らかの物質で満たされていることです。
この二つの条件を備えておれば、それは物体であると認めることにしましょう。こうして
『 物体とは境界面で外部と内部とに分けられ、その内部が物質で満たされているもの 』
と定義します。
物体である条件はとても緩やかなものです。物体がどんな形であるか、その内部はどんな物質で構成されているか、物体が生物であるか非生物であるか、といた事柄には全く関係しません。三つの風景で挙げたすべての物体は、この条件を満足します。
緩やかな条件を用いるのは、できる限り広く物体と認定して、それらの運動を同じ方法で扱いたいからです。以後において、私たちはこの条件に当てはまるものを
物体(
body )と呼ぶことにします。
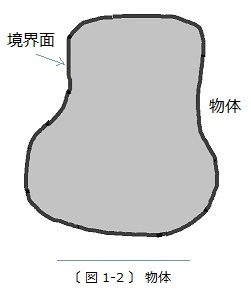
〔 図 1-2 〕 のように、物体を境界面で囲まれた図形として画面に描いて示します。灰色で塗りつぶした図形の内部は、種々の物質で満たされていると想定した物体内部の領域です。
物体は三次元の空間に存在する立体なのですが、それを画面や紙の上で描きたいときには、〔 図 1-2 〕のように、二次元平面の図に置き換えます。ちょうど、画家が対象物をキャンバス上の平面に描くのと同じことです。三次元空間の立体を二次元の平面の図に置き換えて描く方法は、「投影法」と呼ばれます。その概略を述べると、次のようになります (
《 参考資料 1-1 》 ):
対象となる立体を見つめる一つの〝視点〟を導入し、視点、立体、および、(図を描くための)〝平面〟を向かい合わせて空間に配置します。立体の上の各点と視点を結んだ線( これを、「投影線」といいます )と平面との交点が描いたものを「投影図」といいます。この投影図が、立体を二次元の平面に置き換えた図になります。
投影図は二つに大別され、視点が立体と平面から有限の距離に置かれた場合を「中心投影図」といい、視点が無限に離れた距離に置かれた場合を「平行投影図」といいます。
中心投影図は、私たちが対象物を眺めた場合に目に映る像に相当します。〔 図 1-1 〕に示した三つの風景は、そのよう投影図を表したものと言えます。平行投影図では、投影線はすべて互いに平行になります。平面を投影線に垂直に置く「垂直投影」は、制図などで用いられている方法です。互いに 90°ずつ回した三つの平面に投影された図は、「正面図」、「平面図」、「側面図」として知られています。
このホームページでは、これ以後も三次元の立体を二次元の平面に置き換えて描いた図に番号を付けて、〔 図 1-1 〕、〔 図 1-2 〕、〔 図 1-3 〕のように示します。それらの平面の図から、私たちは三次元の立体の像を思い浮かべることが必要になります。例えば〔 図 1-2 〕では、〝境界面〟と書かれた閉じた線は三次元の〝閉曲面〟を表し、灰色で塗りつぶした領域は閉曲面で囲まれた三次元の領域を示します。
物体のいろいろな運動
三つの風景に現れる物体の運動を例にとって、物体はどのように運動するのかを調べてみます。
物体の多くは 〝静止した状態〟にあります。
部屋の中の風景(〔 図 1-1a 〕)では、部屋の床、壁、天井、机、電気コンロ、ヤカンなど、野外の風景(〔 図 1-1b 〕)では、地面、山、道路、、橋、ビルディング、家屋、路上に停止している自動車などです。
上に挙げた以外の物体は 〝動いている状態〟 になっています。
部屋の中でパソコンで作業をしている人、窓から吹き込む風を受けて揺れる蛍光灯、カーテン、床の上を跳ねたり転がってゆくサッカーボール、路上を走行する自動車、上空を飛ぶ鳥、夜空の風景(〔 図 1-1c 〕)では夜空を覆う星などです。夜空を覆う天体は静止した状態に見えますが、長い時間かけて観察すると、天空を少しずつ動いていることが分かります。
同じ物体であっても、静止した状態 であったり 動いている状態 であったりします。自動車は停止しているときは静止した状態にありますが、エンジンをかけて発進させれば運動する状態になります。サッカーボールは、床上で静止した状態であったり、あるいは、床上で跳ねたり転がったりします。
物体のうちで、時間が経過しても〝大きさや形がほとんど変化しない状態〟を保つものがあります。
部屋の床、壁、天井、机、電気コンロ、ヤカン、部屋の天井から吊るされた蛍光灯、野外における地面、山、道路、、橋、ビルディング、家屋、路上に停止している自動車など。その多くは、静止している状態として挙げた物体です。
物体のうち、時間が経過すると〝大きさや形がかなり変化する状態〟になるものがあります。
パソコンで作業をしたり野外を歩いたりする人、窓から吹き込む風を受けて揺れるカーテン、道路の上を走行する自動車、上空を飛ぶ鳥などです。
同じ物体であっても、大きさや形がほとんど変化しないこともあれば、かなり変化することもあります。サッカーボールは、十分に膨らんだ状態にあれば大きさや形がほとんど変化しませんが、萎んだ(ちじんだ)状態では大きさや形がかなり変化します。走行する自動車は、風圧を受けて車体がいくらか変形したり、路面と接触した部分でタイヤが形が変化します。
物体の運動を観察して、四つの運動の状態;
物体が静止した状態、動いている状態、大きさや形がほとんど変化しない状態、大きさや形がかなり変化する状態; に分けました。これらを組み合わせれば
静止していてほとんど変形しない、 動いていてほとんど変形しない、 動いていてかなり変形する
という三つの運動状態になります。ここで〝大きさや形が変化する〟ことを簡潔に〝変形する〟と言い直しました。ただし、静止していてかなり変形する というのは矛盾する運動なので除きました。
変形が全く起こらない物体のことを
剛体(
ごうたい、
rigid body )といいます。実際の物体は多少とも変形するので、剛体は物体を理想化したものです。上述の一番目と二番目の運動については、物体を剛体として近似することができます。したがって、一番目、二番目、三番目の運動は、次のように言い換えられます:
剛体と近似的できる物体が静止している状態、 剛体と近似的できる物体が動いている状態、
変形する物体が動いている状態
三番目の変形が大きい物体の運動は、最も一般的な物体の運動になります。これに対して、変形があまり大きくない物体の運動 (
一番目と二番目の運動 ) は、剛体の運動に類似させて表すことができます。剛体は変形を伴わず形・大きさが保たれるので、その運動をかなり簡単に表すことができます。後の章で改めて説明しますが、剛体が運動する形態は次の二つになります:
一つの形態は剛体の内部の点が平行に移動する運動で、これを「並進( へいしん )の運動」といいます。もう一つの形態は剛体の内部の点が一つの点のまわりに回る運動で、これを「回転の運動」といいます。剛体の一般的な運動は、二つの運動を組み合わせた「並進・回転の運動」になります。
変形があまり大きくない物体の運動 (
一番目と二番目の運動 ) は、三つの風景における物体の運動を例にとると、剛体の運動に類似させて次のように述べられます:
◇ 机、電気コンロ、ヤカン、自動車の車体、自動車のタイヤ、橋、ビルディング、蛍光灯、サッカーボール などは、変形が割合に小さい物体です。これらの物体を近似的に剛体と考えれば、自動車あるいはサッカーボールの運動は並進・回転の運動と見なすことができます。
◇ 自動車が路面に沿って真直ぐに進むとき、自動車の車体は並進の運動になります。自動車が坂を上ったり下ったりするとき、あるいは、平らな路面上でカーブを描きながら進むときは、自動車の車体は並進に回転が加わった 並進・回転運動 になります。自動車が路上を進行するとき、タイヤは車体と一緒に動きながら車軸のまわりに回転する 並進・回転運動を行います。
◇ サッカーボールが床の上でとび跳ねたり床面に沿って転がる運動は、並進と回転が組み合わさった 並進・回転運動 になります。
運動を表す方法
物体の運動を表す方法を説明するにあたって、その方法はどんなものであるべきなのか、あるいは、どんな方法が望ましいのか、という問題を検討することにしましょう。
物体の運動を異なる場所で観察しても、その方法は同じであることが必要です。例えば物体の運動を〔 図 1-1a 〕に示した部屋の中で観察しても、あるいは、〔 図 1-1b 〕に示した野外で観察しても、観察される物体やそれぞれの運動は様々ですが、その運動を表す方法は同じでなければなりません。空間の範囲を広げて、地球上の異なる場所で物体の運動を観察しても、さらには、地球を離れて他の天体や宇宙空間に場所を移したとしても、やはり物体の運動を表す方法は同じでなければなりません。
一方、物体の運動を観察する時間が異なっていても、その方法は同じであることが必要です。現在から後の未来の時間、あるいは、現在を遡った(
さかのぼった )過去の時間で物体の運動を観察しても、その方法は同じでなければなりません。
まとめて述べると、物体の運動を表す方法は
『 この世界のどんな場所にいる人にも、どんな時間においても、共通に用いられる方法 』
であることが必要です。
〝共通に用いられる方法 〟は〝共通に了解できる方法〟でなければなりません。その方法として、数量的な表現を用いるのが良いと考えられます。その方法なら、どんな時間にどんな場所にいる人にも、物体の運動を明確に表すことができるはずです。こうして
『 物体の運動を 数量 を用いて表す方法 』
を用いるのが良い、という結論に到ります。
力学の歴史において画期的な出来事の一つは、物体の運動を数量的に表す方法を採用したことです。その重要性を初めて明確に主張したのは、有名なガリレオ・ガリレイ(1564年-1642年)であると言われています。彼が述べた
『 自然の書物は数学の言葉によって書かれている 』
は良く知られており、しばしば引用されます。《参考資料 1-2 》 には、この文はガリレオの著述した文のなかの一部を抜粋したものと述べられています。
力学において、また物理学において、数量的な表現を用いることは本当に大切なことでしょうか? 私たちが日常で使う言葉と比べて、“数学の言葉“はなじみが少なく、使うのに苦労するのは確かです。それでも、物理学では数量的な表現はどうして頻繁に(
ひんぱんに)使われるのでしょうか? どんな理由で、数量的な表現は重要なのでしょうか? このような問題について、
《 物理学における数量的な表現 》 で改めて検討することにします。
物体の運動を〝観察する〟だけに留まらず、観察された運動を数量で表す方法を用いるとき、その行為を〝観測する〟といいます。さらに機器などを用いて運動を直接に測る方法を用いるとき、その行為を〝測定する〟といいます。
数量を用いて表す方法を採用すると、観測や測定を通して、実際に起きる物体の運動を知ることができます。それによって、計算された物体の運動が正しいものであるか否かを検証することができます。
物体を代表する点
これまで検討した結果として、物体の運動を数量を用いて表すのが良い方法であることが分かりました。しかしながら、複雑な物体の運動をいきなり数量を用いて表そうとするのは困難です。
そこで第一歩として、物体のなかの一つの点だけに注目し、〝その点がどのように運動するのか〟 という問題を考えることから始めます。この点のことを 物体を代表する点 と呼び、この言葉を強調したいときには〈物体を代表する点〉のように カッコ〈 〉で囲って表すことにします
( 注 1-1 )。
〔 図 1-2 〕に示したような物体のなかに、一つの点を選んで〈物体を代表する点〉とすれば、
〔 図 1-3 〕 のようになります。
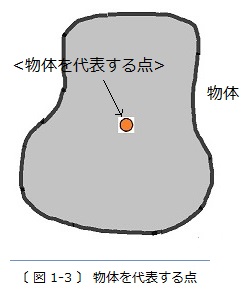
〇 点の大きさは無限小なのですが、その位置を画面で示したいときには、有限の大きさの図形を用いて示さなければなりません。〔 図 1-3 〕では〈物体を代表する点〉を( 内部を濃い灰色で塗りつぶした )丸印で表しました。
ここで〈物体を代表する点〉の位置が何処(
どこ)なのかが問題になりますが、当面はそれを問わないことにします。物体のなかに適当な一つの点を選び、それにマークを付けて、その点を〈物体を代表する点〉とすることにします。〈物体を代表する点〉の位置を定める方法については、後の章(
)で述べることにします。
物体は形と大きさを持っており、並進、回転、変形などが組み合わさった複雑な運動を行います。このような運動を表す方法を見出す代わりに、当面のあいだは(
と では)、物体のなかに選んだ〈物体を代表する点〉の運動だけを考えることにするのです。〈物体を代表する点〉は空間の一つの点なので、それが空間を移動する運動を表す方法は相当に簡単になるはずです。
空間の一つの点の運動を表す方法が見出されたならば、その方法は 並進、回転、変形などが組み合わさった複雑な物体の運動を表す重要な一歩になります。
( 注 1-1 )<物体を代表する点> という言葉を用いましたが、これはホームページの作成者( 揺海 )が名づけたもので、力学の教科書や参考書で一般に用いられている用語でないことを予め断わっておきます。
位置と時間
上述の三つの風景に描かれた物体の運動の例(
身近な風景において物体の運動を観察する)をとり上げて、〈物体を代表する点〉が時々刻々にどのように空間を移動するかを調べてみます。
◇ 人の体の真ん中、例えばお臍あたりにマークを付け、これを〈物体を代表する点〉とします。
人が部屋の中でパソコンに向かって作業しているとき、この点は空間でほぼ静止しています。人が立ち上がって床の上を歩くときには、この点は床面からほぼ同じ高さを保ちながらカーブを描いて空間を運動します。
◇ 自動車の車体のどこか、例えば二つのヘッドライトの中間にマークを付け、これを〈物体を代表する点〉とします。
自動車が路面上で停止しているとき、この点は空間で静止した状態を保ちます。自動車が道路上を走行すると、〈物体を代表する点〉は路面からほぼ同じ高さを保ちながらカーブを描いて空間を運動します。
◇ 夜空に貼り付けられたように見える星は、地球と同程度、あるいは、はるかに大きな天体です。天体はほぼ球形をしており、球の中心付近の点を〈物体を代表する点〉とします。
この点はほとんど静止しているようですが、時間の経過とともに少しづつ空間を移動してゆく運動をします。
これらの例に見られる〈物体を代表する点〉の運動は、次のような簡潔な表現;
『〈物体を代表する点〉の「位置」が、「時間」の経過とともに空間を移動してゆく 』
のように要約することができます。この文では、二つの量が登場します。それは
位置( position )、および、時間( time )
です。物体の運動を表すには、〝数量を用いて表す方法〟が必要であると述べました(
運動を表す方法 を参照)が、ここで〈物体を代表する点〉の運動を表すために「位置」と「時間」の二つの量が現れました。
こうした数量を表すのに、言葉の代わりに、ラテン文字を斜体にしたもの(
イタリック体 )を用いるのが通例になっています。これらを代数式のなかで用いると、主張する内容が簡潔で明瞭に表わされます。「位置」を表すには、イタリック体の
x、
y、
z、または、これらを括弧で囲った (
x,
y,
z ) を用い、時間を表すにはイタリック体の
t を用います。これらの量については、この後に説明します。
位置の座標系
空間における点の「位置」を表すために、まず、その基準となる
座標系(
system of coordinates )を設定します。座標系が設定されたら、それに基づいて空間の点の位置を数量的に表すことができます。
〇 空間の位置を表すために設定する座標系なので、これを強調したいときは「位置の座標系」と言います。通常は〝位置の〟を省略します。
座標系を設定するには、空間において〝静止した状態にある〟と認められる物体を選び出し、そのような物体を基準にして座標系を作り上げます。その座標系は、当然ながら〝静止した座標系〟になります。
座標系として最もよく用いられる標準的なものは、
直交座標系(
orthogonal coordinate system ) です。直交座標系は、空間で静止した点とこれを通る互いに直交する3本の直線でもって構成されます
( 注 1-2 )。この静止した点を座標系の
原点(
origin )といい、3本の直線を座標系の
座標軸(
coordinate axis )といいます。
直交座標系がどのように設定されるかを示すために、例として、〔 図 1-1 〕部屋の中の風景 をとり上げてみましょう。
〔 図 1-4 〕 には、部屋の中の風景(
左図 )から作られる直交座標系(
右図 )を示します:
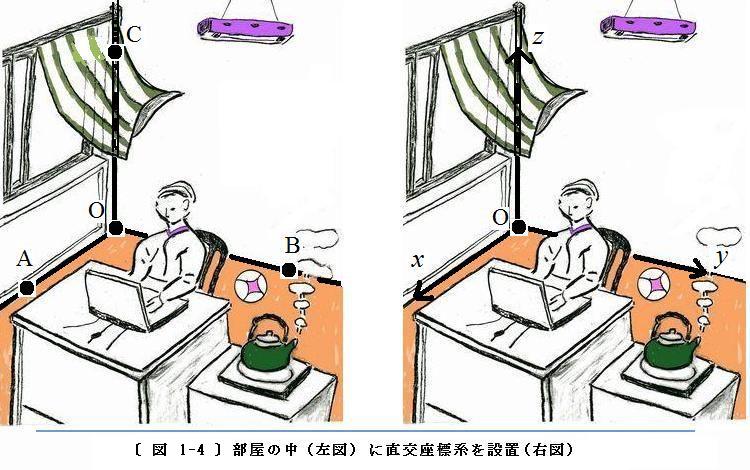
◇ 部屋のなかで机に座っている人から見れば、部屋の床、壁、天井などはすべて静止した状態になっています。床と壁が交わる隅の点も空間で静止した点で、これを 点O とします。O を通り床と窓側の壁が交わる線に沿った直線の上に 点A を、O を通り床と人の背後の壁が交わる線に沿った直線の上に 点B を、O を通り床面に垂直な方向の直線の上に 点C をとります。
◇ O から A に向かう直線、O から B に向かう直線、O から C に向かう直線は、互いにほぼ直交している直線になっています。O を原点、O から A に向かう直線を x 軸、O から B に向かう直線を y 軸、O から C に向かう直線を z 軸 と呼ぶことにします。ここに x、y、z は、ラテン文字を斜体で表したもの( イタリック体 )です。
◇ x 軸、y 軸、z 軸 の3本の直線を直交座標系の 座標軸 として用い、これに 原点O を含めれば、直交座標系 が作り上げられます。直交座標系を図に描いて示したいときは、それぞれの座標軸を先端に矢印を付けた線分で表し、矢印の近くに座標軸の名前 x、y、z を付記するのが通例です。これを〔 図 1-5 〕の右図に示します。矢印の向きを座標軸の〝正の方向〟といい、矢印と反対の向きを座標軸の〝負の方向〟といいます。
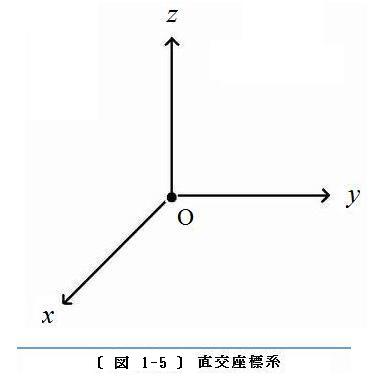
〔 図 1-4 〕の右図から物体をすべて取り去れば、原点O と
x 軸、
y 軸、
z 軸 から成る3本の座標軸だけが残されて、
〔 図 1-5 〕 のようになります。直交座標系は、原点 O と3本の座標軸の文字を並べて O
xyz とし、これを括弧で囲った記号;
( Oxyz )
で簡潔に表すことができます。
〔 図 1-5 〕の左図に示した3本の直線;
O から A に向かう直線
O から B に向かう直線
O から C に向かう直線
は、正確には互いに直交している直線でないかも知れません。その場合には、測量を行って三つの座標軸;x 軸、y 軸、z 軸;が互いに直交するように座標軸の向きを修正することができます。修正した座標軸を用いれば、座標軸が互いに直交する正確な直交座標系( Oxyz )が設定されます。
3本の座標軸の向きの組み合わせに応じて、直交座標系は「右手系」と「左手系」に分類されます (
《 参考資料 1-3 》 ) 。
・ 右手を原点の位置に置き、親指・人差指・中指を互いに直角になるように曲げて、親指を x 軸 の正の方向に、人差指を y 軸 の正の方向に向けたとき、中指の差す方向が z 軸 の正の方向に一致するとき、この座標系を「右手系」といいます。
・ 右手に代えて左手を用い、親指と人差指を右手系の場合と同じ座標軸の正の方向に向けたとき、中指の差す方向が z 軸 の正の方向に一致するとき、この座標系を「左手系」といいます。
右手系と左手系のどちらを用いても構わないのですが、多くの場合に右手系が用いられます。このホームページでも、〔 図 1-5 〕に示すような右手系の直交座標系を用いることにします。
( 注 1-2 ) 直交座標系( Oxyz )は、デカルト座標系( Descartes coordinates )とも呼ばれます。
位置座標
直交座標系( O
xyz )が設定されているとき、以下のような方法を用いて、空間の点の位置を数量的に表すことができます。
空間の 点 P の位置から、直交座標系( O
xyz )の
x -
y 平面、
y -
z 平面、
z -
x 平面に垂線を下ろし、その足の位置を それぞれ B、D、C とします。ここに
◇ x - y 平面;x 軸 と y 軸 が作る平面
◇ y - z 平面;y 軸 と z 軸 が作る平面
◇ z - x 平面;z 軸 と x 軸 が作る平面
です。
P を通る
x -
y 平面に平行な面、
y -
z 平面に平行な面、
z -
x 平面に平行な面は、それぞれ、
x 軸 と 点 Q で、
y 軸 と 点 R で、
z 軸 と 点 S で交わります。
〔 図 1-6a 〕 に、これを示します。
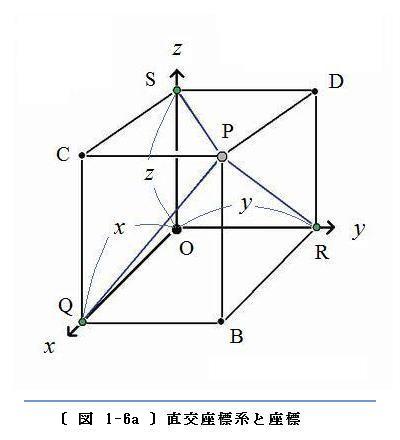
◇ Q、R、S の位置は、直接に P から x 軸、y 軸、z 軸 の上に垂線を下ろしたときの足の位置と同じです。このことは、簡単に確かめられます。
原点O から 位置 Q、R、S までのあいだの
長さ(
length )を測ると、それぞれ、
x、
y、
z であったとします。これら3つの量
x、
y、
z のそれぞれを、位置Pの
x 座標成分、
y 座標成分、
z 座標成分
といい
( 注 1-3 )、3つの量の間にコンマ(,) を入れてカッコで囲ったもの;
(
x,
y,
z )
を 位置 P の
座標 (
coordinates ) といいます。
〇 空間の位置を表す座標なので、これを強調したいときは「位置座標」と言います。通常は〝位置〟を省略します。
空間の一つの点 P の位置は、このように 座標(
x,
y,
z )を用いて数量的に表されます。空間の点の位置 および 座標は、〝1対1〟 に対応します。すなわち、空間の点 P の位置を与えれば一通りの座標(
x,
y,
z )が定まり、これとは逆に、座標(
x,
y,
z )を与えれば空間の点 P の位置が一通りに定まります。
〔 図 1-6a 〕には、Q、R、S の位置がいずれも座標軸の正の側(
矢印の指す方向 )にある場合を示しました。これらの位置が座標軸の負の側(
矢印の指す向きと反対の方向)にある場合は、原点から垂線の足の位置までの距離(
長さ )にマイナスの符号を付け、これを座標成分と定めることにします。
◇ 座標成分の符号をこのように定めると、x 座標成分 、y 座標成分、z 座標成分 の各々は、プラス(+)または マイナス(-)の量になります。座標( x,y,z )の符号だけを抜き出して示せば、その組み合わせは
(+,+,+)、(+,+,-)、(+,+,-)、(+,-,-)、
(-,+,+)、(-,+,-)、(-,+,-)、(-,-,-)
の8通りになります。〔 図 1-6a 〕に示した P の座標は、1番目の(+,+,+) の場合になります。8通りの符号を有する座標( x,y,z )は、空間を8つの領域に分割します。それぞれの領域は「象限」と呼ばれ、順番に番号を付けて 第1象限、第2象限、…、第8象限 といいます。
直交座標系( O
xyz )を用いて空間の点の位置を表す方法を説明しましたが、これ以外にもいくつかの座標系があります。よく用いられるものに
円柱座標系(
cylindrical coordinates )と
球座標系(
spherical coordinates )(
球面座標系 ともいう) があります。この二つの座標系について
《 円柱座標系 と 球座標系 -その1- 》 で説明します。
( 注 1-3 )位置Pの x 座標成分、y 座標成分、z 座標成分 という代わりに、位置Pの x 軸成分、y 軸成分、z 軸成分、あるいは、簡単に x 成分、y 成分、z成 分 ともいいます。なお、座標軸の名前と座標成分を同じ文字の x、y、z で表すのが慣例になっています。
時間の座標系と時間座標
空間の点の位置を〝座標系と座標〟を用いて数量的に表しましたが、同じようにして、時間を数量的に表すことができます。
〔 図 1-7 〕 に示すように、平面の上に左から右に向けて1本の座標軸を描き、その右端に矢印を付けます。この座標軸の上に基準となる一つの点 O
t をとり、これを「時間の座標系の原点」とします。
〇 座標軸は無限に長い直線ですが、図面では直線を有限な長さの線分で置き換えて描きます。
〇 座標軸の原点には、時間を表す意味で O に添字の t を付けました。また座標軸の右端には、座標軸の名前を示すために文字 t を表記しました。
このように、平面に描いた1本の座標軸および座標軸上の原点でもって「時間の座標系」が作られます。〔 図 1-5 〕の例に示したように、位置の座標系は空間に存在する静止した諸物体を基準にして設定されました。これに対して、時間の座標系は平面上の図形で表した思考的なものです。
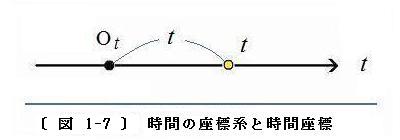
ある一つの「時刻」をイタリック体の
t で表し、〔 図 1-7 〕の座標軸の上で原点 O
t から距離が
t だけ離れたところに 点(
黄色の丸印で示す )をとります。この点が「時間座標」で、その点の傍に時刻
t を記します。時間座標
t に符号を付け、その点が 原点の O
t から矢印の向く側にあるときは プラス(+)とし、矢印の向きと反対側にあるときは マイナス(-)とします。
〇 〔 図 1-7 〕で原点から時刻 t に至る線分の長さは、時刻が 0(ゼロ)から時刻 t までに経過した〝時間の長さ〟を表しています。これを「時間」といいます( 注 1-4 )。
( 注 1-4 ) 実際には〝時刻〟と〝時間〟という言葉は、それほど厳格には使い分けられていません。しばしば〝時刻〟と言うべきところを〝時間〟と言ったりします。
〈物体を代表する点〉の運動 -位置座標を時間の関数として表す-
位置と時間を数量的に表すために、〝位置の座標軸と位置座標〟、および、〝時間の座標軸と時間座標〟を設定しました。これらを用いて、〈物体を代表する点〉(
〈物体を代表する点〉 および〔 図 1-3 〕を参照)の運動を次のように表します。
〈物体を代表する点〉の運動は、『 その位置(
x,
y,
z )が時間
t とともに空間を移動してゆくこと 』と述べられます(
位置と時間 を参照)。観察される運動を、位置と時間という二つの量のあいだの関係に置き換えたのです。さらに、二つの量の関係を直接に示して
『 時間
t にいろいろな値を与えると、それに応じて座標成分
x、
y、
z の値が次々に定まる 』
とします。時間と座標のようにその値が変化する量のことを、数学では〝変数〟といいます。変数
t と変数
x、
y、
z のこのような関係は、数学では
『 変数 x、y、z は変数 t の 関数( function)である 』
と簡潔に言い表します。このとき変数
t を「独立変数」といい、変数
x、
y、
z を「従属変数」といいます。
◇ 独立変数 t の値を与えると、それに応じて従属変数 x の値が定められる明確な関係が存在するとき、数学では『 x は t の関数である 』といい、このことを記号で
x ( t )
と表示します ( 注 1-5 )。
〈物体を代表する点〉の座標は、このように時間
t の関数として
( x ( t ), y ( t ), z ( t ) )
と表されます。物体を代表する点〉の運動は、この簡潔な形式を用いて数量的に表されます。
このページ(
)の冒頭に示した諸物体の運動の例(
〔 図 1-1a 〕〔 図 1-1a 〕、〔 図 1-1a 〕)では、様々な運動が観察されます。物体の運動を〈物体を代表する点〉の運動に置き換えると、それらすべては、上記の (
x (
t ),
y (
t ),
z (
t ) ) という一つの形式に要約されます。これは実に簡明な結論です。ニュートン力学、さらには他の分野の電磁気学、熱力学、量子力学、相対性理論においても、種々の物理量を関数の関係として結び付ける方法が多用されます。
簡単な関数は日常においてよく用いられますが、それは実際の現象を表すモデルとして、あるいは近似的に表そうとする場合にも便利に用いられます。例として、「一次関数」、「二次関数」、「指数関数」、「対数関数」、「べき関数」、「三角関数」を
《 簡単な関数 》 に示します。
( 注 1-5 )x が t の関数であるとき、この関係は文字 f を用いて
x = f( t )
のように表されることもあります。そのように表す代わりに、独立変数 t と従属変数の x を直接に結び付けて x( t )と表すこともあります。後者は便利な表し方なので、このホームページでは主にこの表し方を用いることにします。
〈物体を代表する点〉の運動を図に表す -その1-
〈物体を代表する点〉の運動は、座標を時間の関数として (
x (
t ),
y (
t ),
z (
t ) ) のように表されますが、この運動を図面に描くと分かり易いでしょう。
運動は 初めの時刻
ts から始まるとし、この時刻を
初期時刻 といいます。時刻
t を 初期時刻
ts に選んで座標に代入すると、(
x (
ts ),
y (
ts ),
z (
ts )) となりますが、これは初期時刻における〈物体を代表する点〉の空間の位置 P
s を示します。
時刻が
ts から増加してゆくと、各々の時刻における (
x (
t ),
y (
t ),
z (
t )) は、次々に空間の点を占めてゆきます。時間
t が連続的に変化したとき、それに応じて定められる空間の点の位置も
連続的に変化する と仮定します。
◇ この仮定が成立するためには、従属変数 x、y、z が独立変数 t の「連続関数」であることが必要です。
時間の変化とともに空間に作られる線(
一般には曲線)のことを、〈物体を代表する点〉の
軌道(
orbit )といいます。軌道は滑らかな曲線であることが必要です。
◇ この仮定が成立するためには、関数
x (
t )、
y (
t )、
z (
t ) が いずれも変数
t について「微分可能」であることが必要条件です。これについては後ほど改めて説明します(
)。
〈物体を代表する点〉は、初めの時刻
ts から出発し、時間の経過とともに空間の各点を辿り(
たどり)、ある時刻
t において空間の点 P に至るものとします。
〔 図 1-8a 〕 に、座標成分
x、
y、
z を定める基準となる直交座標系( O
xyz )、初期時刻
ts の位置 P
s を示す座標 (
xs (
t ),
ys (
t ),
zs (
t ) )、時刻
tの位置 P を示す座標 (
x (
t ),
y (
t ),
z (
t ) ) 、および、P
s と P を結ぶ軌道の曲線(
太い茶色の線で)を示します。〔 図 〕には代表として軌道上の二つの点 P
s と P だけを示しましたが、もちろん、途中の任意の時刻における点の位置も同様に座標で示されます。
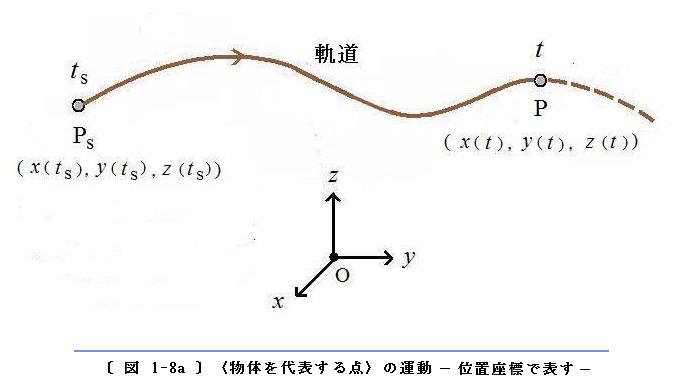
〈物体を代表する点〉の軌道は、〔 図 〕のように、いつも連続で滑らかな曲線を描くものと考えられます。
長さと時間の単位
位置の座標成分は、〝空間における長さ〟 として、時間座標は〝経過する時間の長さ〟として実測できるで量です。これらの量を測定するときには、ともに基準となる
単位(
unit ) を用いて表されます。長さについては「長さの単位」が、時間については「時間の単位」が用いられます。
古くから世界の各地において、日常で用いられる量について人々が共通に了解できる方法で単位を定めてきました。現在では、国際的に共通な基準として定めた
国際単位系( 略して
SI )の単位が広く用いられるようになりました。
国際単位系( SI )における長さの単位は、日本文字 または 立体のラテン文字で
メートル、または、m
と表され、時間の単位は
秒、または、s
と表されます( m は metre の頭文字、s は second の頭文字です)。このホームページでは、長さの単位と時間の単位として m と s の文字を用い、[ ] で囲って [ m ] と [ s ] のように表示することにします。
時間の単位と長さの単位に関する補足的な説明を
《 時間の単位 および 長さの単位 》 に示します。
座標成分
x、
y、
z のそれぞれの大きさは、長さの単位 [ m ] の何倍であるかを示せば指定できます。〝何倍である〟というのは〝実数〟で表すことができるので、座標成分
x、
y、
z のそれぞれは、実数と m の積、すなわち
実数 [m]
のように表されます。同様に時間の大きさは、実数と時間の単位の積;
実数 [s]
のように表されます。実数は、プラス(+)または マイナス(-)の符号をとります。
私たちは、日常で〝空間〟という言葉を使います。それでは『 空間とは一体どんなものなのか? 』と改めて尋ねられると、即座に答えるのは容易ではありません。けれども、『 ニュートン力学では空間をどんなものと規定するのか? 』と尋ねられたら、それには次のように答えることができます。ニュートン力学では、以下に説明するような〝ユークリッド空間〟 を定義し、そのような空間で物体は運動を行うとするのです。
空間に直交座標系を設定し、空間の点の位置を座標として表した方法を振り返ってみます。それは次の順序で行われます:
- 空間に存在する諸々の物体から、静止している物体を選び出す。
- 選び出した物体を基準にして、〔 図 1-6 〕に示すような直交座標系( Oxyz )を設定する。
- 空間のなかに、任意の一つの点 P を指定する。
- 〔 図 1-7a 〕の図形的な操作によって、点 P に位置から3個の座標成分 x、y、z が定められる。
- 座標成分は、実数と長さの単位 m との積;x ={ x の実数値 }[m]、y ={ y の実数値 }[m]、z ={ z の実数値 }[m];の形に表される。ゆえに座標成分の x、y、z から、{ x の実数値 }、{ y の実数値 }、{ z の実数値 } が定められる。
この操作を〝1番目の方法〟ということにします。ここで上記の3番目から5番目までの過程を逆にして、次のような操作に換えてみましょう:
- 3個の { x の実数値 }、{ y の実数値 }、{ z の実数値 } を指定する。
- これらの実数値に長さの単位をかければ、x ={ x の実数値 }[m]、y ={ y の実数値 }[m]、z ={ z の実数値 }[m] となり、三つの座標成分が作られる。
- 〔 図 1-7a 〕の図形的な操作を逆にたどれば、3個の座標成分 x、y、z から空間の一つの点 P の位置が定められる。
この操作を〝2番目の方法〟ということにします。〝1番目の方法〟では、初めに空間の一つの点 P の位置を指定すると、{
x の実数値 }、{
y の実数値 }、{
z の実数値 } が定められます。〝2番目の方法〟では、初めに{
x の実数値 }、{
y の実数値 }、{
z の実数値 } を指定すると、空間の一つ点 P の位置が定められます。二つの操作は〝1対1〟に対応します。
〝2番目の方法〟を用いて、次のような思考上の操作を行います:
◇ { x の実数値 }、{ y の実数値 }、{ z の実数値 } のそれぞれに値を代入し、それらに長さの単位 [m] をかけると、座標( x,y,z )ができます。この座標と〝1対1〟に対応する点を空間にプロットします。
◇ 3個の実数値に、プラス、ゼロ、マイナスを含めたすべての可能な値を代入し、それらに長さの単位 [m] をかけます。こうしてできる座標と〝1対1に対応する点〟を空間にプロットすると、実数の連続性から、空間のあらゆる領域はこれらの点の集まりで隙間なく連続的に埋め尽くされます。
思考によって生み出されるこのような点の集まりが空間を作ると考え、これを
ユークリッド空間 (
Euclidean space ) と定義します。ユークリッド空間は、ユークリッド幾何学の定理に基づく図形的な操作、および、実数の連続性を用いて数量的に作り上げた空間です。
・空間にユークリッドという名を冠するのは、古代エジプトのギリシャ哲学者エウクレイデス(英名 Euclid、ユークリッド)の著書の「原論」で論じられた「ユークリッド幾何学」を用いて作られる空間であるからです。
ユークリッド空間における直線、面、立体などの空間図形は、3個の実数値; {
x の実数値 }、{
y の実数値 }、{
z の実数値 }; に適当な制限を課すことによって作り上げられます。その簡単な例を
《 簡単な空間図形 》 に示します。
もともと自然は人間の思考とは無関係に存在するものであり、それを〝ユークリッド空間である〟と規定するのは人為的で不自然ではないか、と思われるかも知れません。
しかしながら、物体の運動を数量を用いてこの世界で共通した方法で表そうとするならば、物体が運動する空間を何らかの数量的なやり方で表すことが必要になります。ユークリッド空間は、ユークリッド幾何学および実数の連続性を用いて数量的に作り上げた空間です。地表面の地形、建物、構造物、手元の道具といった身近な物体の図形的な関係は、ユークリッド幾何学を用いて解析され、その結果は実測されたものに良く合います。もう一つの実数の連続性は、連続的に変化する数量を扱うときに用いられる基本的な条件です。
ニュートン力学では、ユークリッド空間において物体が運動するものと仮定します。この力学を用いて物体の運動を計算すると、少なくとも私たちの身近な地表面の付近で起きる広範な現象については、十分に良い精度で観測され測定された結果に良く一致することが確かめられています。
〇 ユークリッド空間は、ユークリッド幾何学を基礎にして定義された空間です。この幾何学を別の幾何学に置き換えたなら、それに基づいて定義される空間は、ユークリッド空間ではない別の空間になります。
数量的に定義した空間は、そこに存在する物体を基準にして設定した直交座標系から作り上げられた空間です。空間と座標系は結びつけられて定義されるので、この関係を明示したいときには
『 座標系( O
xyz )の空間 』
といいます。もし物体を別のものに選べば、それを基準にして設定する座標系も別のものになり、したがって別の空間が作り上げれれます。そのため同じ物体の運動が、ある空間と別の空間では異なった運動として表されるという事態が起こります。これは「相対運動」と呼ばれる力学の重要な問題ですが、これについては後の章で改めて詳しく説明することにします。
ニュートン力学における時間、空間、物体
ニュートン力学では、時間と空間、および、物体をどのように捉えて( とらえて )いるのでしょうか。第1章の《第一ステップ》の最後に、これを簡単に整理しておきます。
時間については、過去から未来に向かって一様に流れるものであり、この世界のどんな場所においても時間の流れは変わらないものと考えます。
空間については、世界に存在する諸物体をそのなかに収容できる無限に大きな容器のようなものであり、もし物体を次々と取り除いてゆくと、やがては空虚な真空のような存在になるものと考えます。
物体が空間に存在すると、物体を構成している点の集まりは空間のある領域を占めます。物体の運動は、こうした物体を構成している点の集まりが時間とともに空間を移動してゆく現象です。第1章ではその第一歩として、『 物体の位置を <物体を代表する点>の位置 で表す 』という簡単な方法を採用しました。<物体を代表する点>の運動は、その位置の時間的な変化として表されます。
空間と時間とはそれぞれ独立な存在であり、互いに影響を及ぼすことはない、と考えるのは当然であると思われます。空間に収容された諸々の物体のそれらの存在が、過去から未来に向けて流れる時間に何らかの変化を及ぼすとは考え難いことです。
ところが、20世紀初頭にアインシュタインが提唱した特殊相対性理論では、ニュートン力学では当然であるとしたこの前提を覆しました。その新しい理論では、時間座標の一つと空間の座標成分の三つを併せた4つの座標成分は、互いに関連させて扱う必要があることが示されました ( 《 参考資料 1-4 》 )。時間と空間はもはや独立した存在ではなく、互いに密接に関係します。
相対性理論はニュートン力学よりも一般性を有する理論で、相対性理論から見れば、ニュートン力学はある条件の下で〝近似的に成立する力学〟になります。私たちの地球の表面付近で起こる非常に多くの様々な現象については、幸いなことに、時間と空間を独立に扱うニュートン力学を用いて十分に良い精度で説明することができます。この問題については、後の章において改めて述べることにします。
◇ 《 参考資料 1-1 》
フリー百科事典ウィキペディア(Wikipedia)、「投影図」、http://ja.wikipedia.org/wiki/%E6%8A%95%E5%BD%B1%E5%9B%B3。
◇ 《 参考資料 1-2 》
朝永振一郎著、「物理学とは何だろうか」上巻、下巻、岩波新書、1979年5月第1刷、1979年12月第3刷発行: 上巻 p.82-83。
◇ 《 参考資料 1-3 》
矢野健太郎・茂木 勇・石原 茂編著、「数学小辞典」、共立出版株式会社、1968年初版1刷、2000年初版55刷発行: p.522。
◇ 《 参考資料 1-4 》
佐藤勝彦著、「相対性理論」、岩波基礎物理シリーズ9、株式会社 岩波書店、1996年第1刷、2000年初版55刷発行: 1-210p。
《 改定 第1章 ―第1ステップ― 》では、一つの物体を〈物体を代表する点〉で代表させるという簡単な方法を採用して、この点の運動を数量的に表す方法を示しました。その概要は次のようです:
空間に座標系を設定し、空間の点の位置を座標として表します。〈物体を代表する点〉は空間の点なので、その位置もまた座標で表されますが、それは時間とともに一般には空間を移動します。このことを『 〈物体を代表する点〉の位置は時間の関数である 』と言い表します。こうして、〈物体を代表する点〉の運動を「時間」と座標で表した「位置」を用いて数量的に表す方法が与えられます。
次の
では、別の方法として、〈物体を代表する点〉の運動を「ベクトル」と呼ばれる量を用いて表す方法について説明します。
このページの
トッップヘ
 (a)部屋の中の風景
(a)部屋の中の風景 野外では、すぐ近くを高速道路が通っています。それは川を超えて遠くに立ち並ぶビルディングの方向へ伸びています。道路の脇には常緑樹の大きな樹木があり、高速道路の上を乗用車、トラック、バスなどの自動車が次々と走行してゆきます。一般道路の上には、停車していたり走行する自動車が見られます。川の水は左方にゆったりと流れ、川の上には橋が架かっています。
野外では、すぐ近くを高速道路が通っています。それは川を超えて遠くに立ち並ぶビルディングの方向へ伸びています。道路の脇には常緑樹の大きな樹木があり、高速道路の上を乗用車、トラック、バスなどの自動車が次々と走行してゆきます。一般道路の上には、停車していたり走行する自動車が見られます。川の水は左方にゆったりと流れ、川の上には橋が架かっています。 (c)夜空の風景
(c)夜空の風景 と定義します。
と定義します。

 3本の座標軸の向きの組み合わせに応じて、直交座標系は「右手系」と「左手系」に分類されます (
3本の座標軸の向きの組み合わせに応じて、直交座標系は「右手系」と「左手系」に分類されます ( 
 ある一つの「時刻」をイタリック体の t で表し、〔 図 1-7 〕の座標軸の上で原点 Ot から距離が t だけ離れたところに 点(
ある一つの「時刻」をイタリック体の t で表し、〔 図 1-7 〕の座標軸の上で原点 Ot から距離が t だけ離れたところに 点( 